Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 2 - Encontro 1 /U2S1 - Atividade Diagnóstica
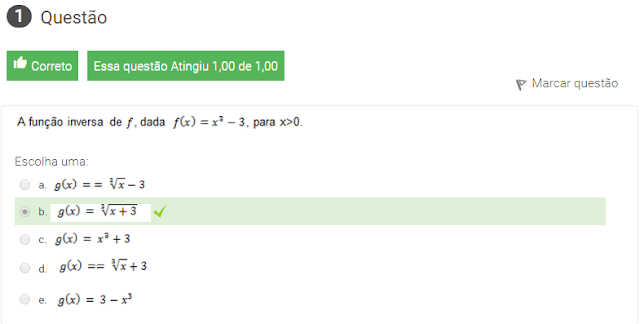
1 a função inversa de f, dada f(x)=x²-3, para x>0
3 O volume do sólido obtido girando-se em relação ao eixo y, a região limitada pelas retas y = 0, y = 2 e y = x – 2 é :
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 2 - Encontro 2 /U2S2 - Atividade Diagnóstica
1 o valor da integral int _0^1:6x²(x³+2)^2dx é:
2 O valor da integral int _1^0:2xInx²dx
essa numero 2 a resposta n é 0 e nem 1 boa sorte em fazer essa n consegui fazer :)
3 O valor da integral int _0^{pi }:senxcosxdx:é:
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 2 - Encontro 2 /U2S2 - Atividade de Aprendizagem
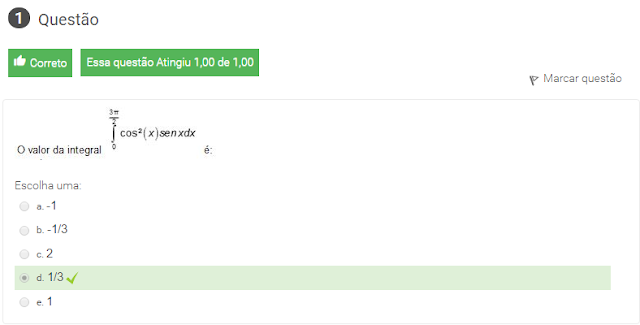
1 0 valor da integral int 0^3pi }{2}cos^2(x)senxdx
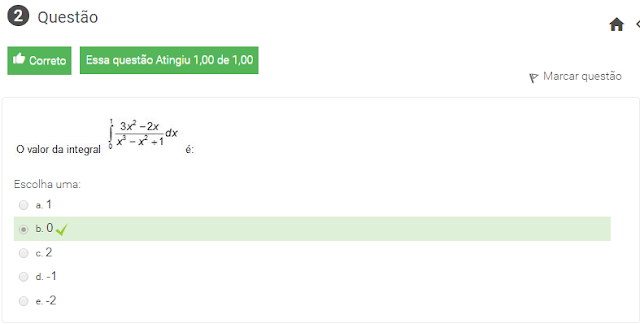
2 0 valor da integral int 0^1{3x²-2x}{x^3-x²+1}dx
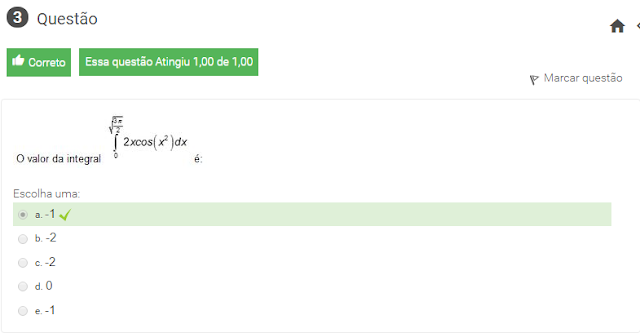
3 0 valor da integral int 0^3pi }{2}2xcos(x²)dx
4 0 valor da integral int pi {2}^{3pi }{2}2e^xcosxdx
5 0 valor da integral int {e²}^{e³}ln(x)dx
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 2 - Encontro 3 /U2S3 - Atividade Diagnóstica
1 Determine a coordenada cartesiana do ponto P(- π/6 ,3).
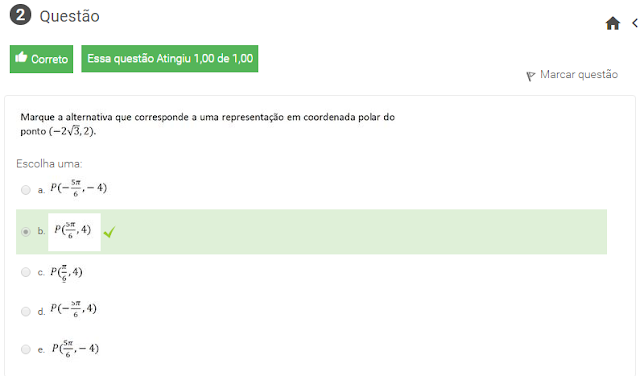
2 marque a alternativa que corresponde a uma representação em coordenada polar do ponto (-2 raiz 3,2).
3 o valor da integral int 0^{pi }sinxcosxdx
essa 3 a resposta não é a letra "d"e nem a letra "e" !!!
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 2 - Encontro 3 /U2S3 - Atividade de Aprendizagem
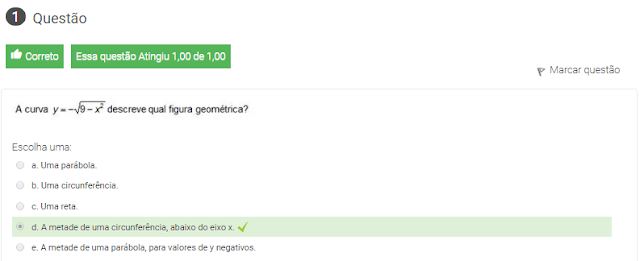
1 a curva y=-raiz 9-x² descreve qual figura geometrica
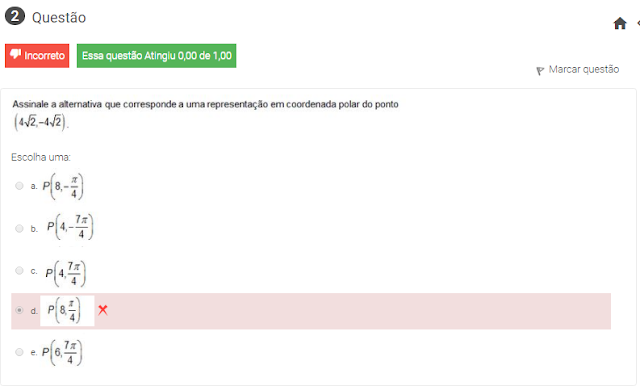
2 assinale a alternativa que corresponde a uma representação em coordenada polar do ponto (4raiz2,-4raiz2)
3 assinale a alternativa que corresponde a uma representação em coordenada polar do ponto (3,3raiz3)
4 a curva polar r=3 e descrita em termos de coordenadas cartesianas pela equação:
5 Determine a coordenada cartesiana do ponto p(2,-pi/3)em coordenadas polares.
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 2 - Encontro 4 /U2S4 - Atividade Diagnóstica
1 Calcule a área entre a curva descrita pela função y(x)= 2/ raiz de 2-x ao quadrado e o eixo x, no intervalo
2 resolva a integral de 0 a 3 (3/raiz de 9-x²) dx
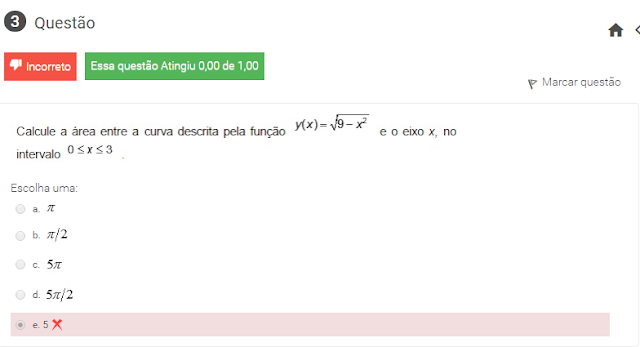
3 Calcule a área entre a curva descrita pela função y(x)=raiz 9-x² e o eixo x, no intervalo
A resposta dessa "3" não e 5 e nem 5pi/2 BOA SORTE :)
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 2 - Encontro 4 /U2S4 - Atividade de Aprendizagem
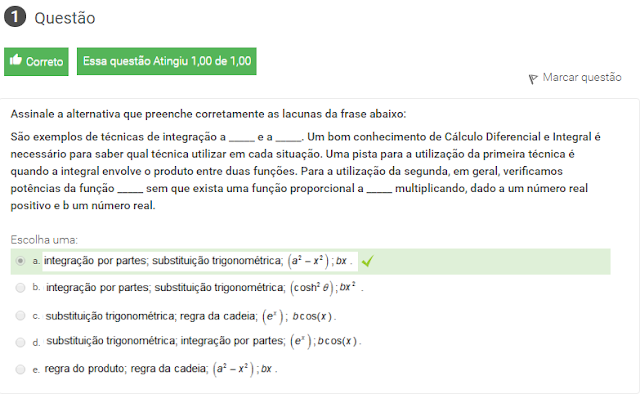
1 Assinale a alternativa que preenche corretamente as lacunas da frase abaixo:
São exemplos de técnicas de integração a _____ e a _____. Um bom conhecimento de Cálculo Diferencial e Integral é necessário para saber qual técnica utilizar em cada situação. Uma pista para a utilização da primeira técnica é quando a integral envolve o produto entre duas funções. Para a utilização da segunda, em geral, verificamos potências da função _____ sem que exista uma função proporcional a _____ multiplicando, dado a um número real positivo e b um número real.
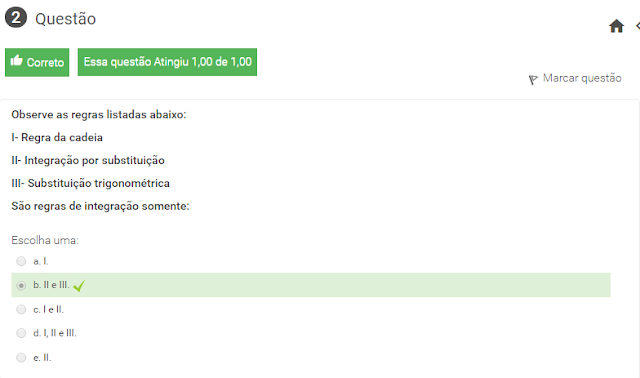
2 Observe as regras listadas abaixo:
I- Regra da cadeia
II- Integração por substituição
III- Substituição trigonométrica
São regras de integração somente:
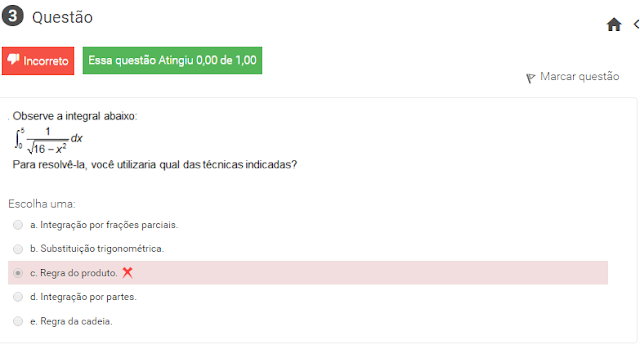
3 observe a integral abaixo para resolve-la , voce utilizara qual das tecnicas indicadas ?
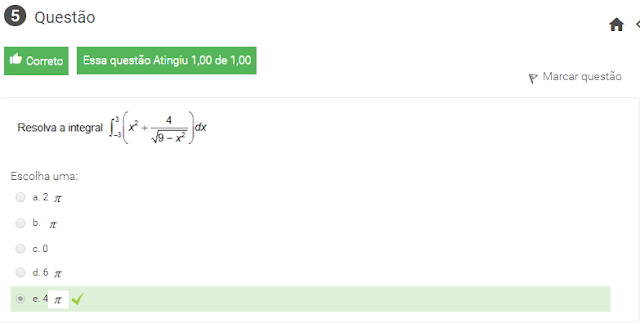
4 resolva a integral int _{-3}^3left(x²+ rac{4}{sqrt{9-x²}} ight)dx
5 Calcule a área entre a curva descrita pela função y(x)=5/raiz 9-x² e o eixo x, no intervalo 0<= x <=3.
nessa 5 eu acho q a resposta certa e 5pi/2 eu acho :)
prova tipo 2
1 resolva a integral 0a3 (2+3/raiz9-x²)dx
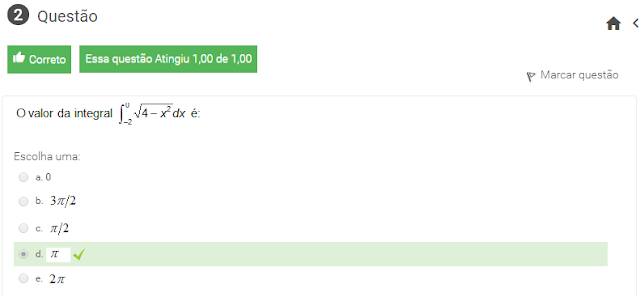
2 o valor da integral de -2a0 raiz4-x² dx é:
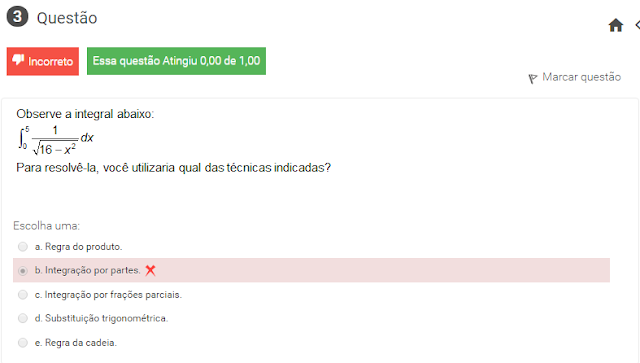
3 Observe a integral abaixo ∫_0^5 (1/√9-x^2)dx para resolvê-la, você utilizaria qual das técnicas indicadas?
não é regra do produto e nem integração por partes
4 observe a integral abaixo de 0a5 1/raiz 16-x² dx
5 resolva a integral de -3a3 (x²+4/raiz9-x²)dx
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 2 - Encontro 4 /U2 - Avaliação da Unidade
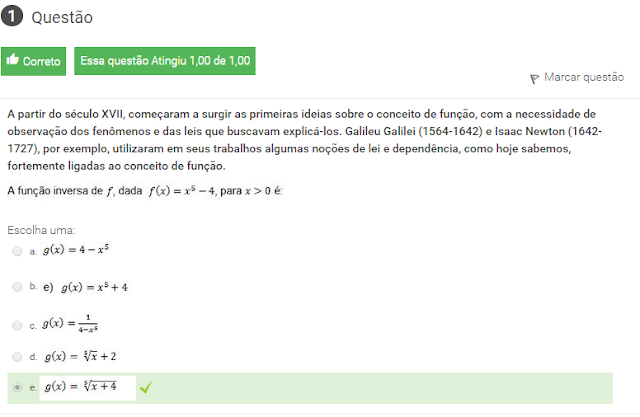
1 A partir do século XVII, começaram a surgir as primeiras ideias sobre o conceito de função, com a necessidade de observação dos fenômenos e das leis que buscavam explicá-los. Galileu Galilei (1564-1642) e Isaac Newton (1642-1727), por exemplo, utilizaram em seus trabalhos algumas noções de lei e dependência, como hoje sabemos, fortemente ligadas ao conceito de função.
A FUNÇÃO INVERSA DE F DADA f (X) = x^5 -4 para x>0 é?
2 “Geometria é ‘compreender o espaço’. Compreender o espaço em que a criança respira, se move. O espaço que a criança deve aprender a conhecer, explorar, conquistar, de modo a poder aí viver, respirar e mover-se melhor. [...] A geometria presta-se, mais do que outros temas, para a aprendizagem da matematização da realidade e para a realização de descobertas, que, sendo feitas também com os próprios olhos e mãos, são mais convincentes e surpreendentes.” (Hans Freudenthal. The Case of Geometry.)
3 Como consequência do Teorema Fundamental do Cálculo de Newton, as integrais foram simplesmente vistas como derivadas "reversas". Na mesma época da publicação das tabelas de integrais de Newton, Johann Bernoulli descobriu processos sistemáticos para integrar todas as funções racionais, que é chamado método das frações parciais. Essas ideias foram resumidas por Leonard Euler, na sua obra sobre integrais.
4 Após o estabelecimento do Cálculo, Euler daria continuidade ao estudo de funções ‒ ainda prematuro na época ‒ juntamente com Cauchy, Gauss e Riemann. Foi Euler, entretanto, quem reuniu todo o conhecimento até então desenvolvido e criou os fundamentos da Análise.
5 A coordenada polar é uma ideia simples surgida nos trabalhos de René Descartes e Pierre de Fermat, no século XVII, que, em conjunto com o Cálculo, permite investigar as propriedades das curvas por meio das ferramentas da Álgebra.