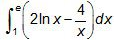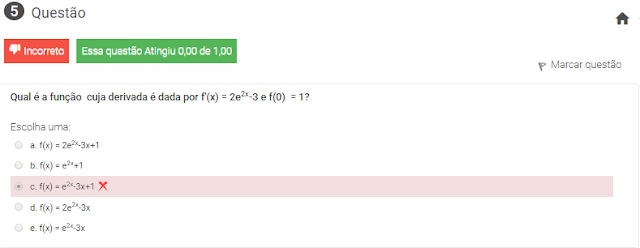Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 1 - Encontro 1 /U1S1 - Atividade Diagnóstica
1 A função que é uma primitiva de f(x) = x2+3 é:
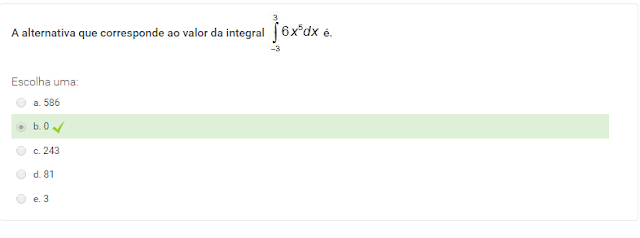
2 A alternativa que corresponde ao valor da integral 
é:
3 Em uma fábrica de móveis querem descobrir a área de uma peça de madeira que pode ser modelada pela região limitada entre as retas y=0, x=2 e pela curva y=x3/2. Qual é o valor dessa área?
1 Faça uma estimativa inferior da área entre o gráfico da função 
e o eixo x, limitado pelas retas x=0 e x=1. Utilize 5 retângulos com base 0,2. O valor estimado da área é:
2 O valor da área da região limitada pelas retas y=0, x=-2, x=2 e pela curva 
é:
3 A alternativa que corresponde ao valor da integral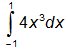 
é:
4 A alternativa que corresponde ao valor da integral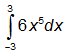 
é.
5 Marque a função que é uma primitiva de 
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 1 - Encontro 2 /U1S2 - Atividade Diagnóstica
1 Uma primitiva para f(x) = 2sen(3x) - 3x2 é:
2 Marque a alternativa que corresponde ao valor da integral a seguir:
3 Um carro começa a acelerar segundo a equação 
. Marque a alternativa que corresponde à variação da velocidade nos 6 primeiros segundos. Dado: aceleração é a taxa de variação da velocidade com relação ao tempo.
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 1 - Encontro 2 /U1S2 - Atividade de Aprendizagem
1 Marque a alternativa que corresponde à integral indefinida de f(x) = 6x5-3cos(x).
2 A área entre as retas x=e, x=e2, y=0 e a curva y(x) = ln(x) é:
3 Uma primitiva para 
é:
4 A alternativa que corresponde ao valor da integral a seguir é:
5 Uma primitiva para f(x) = 4x3 - 3com(3x) é:
Segundo tipo de prova
1 Uma primitiva para 
é
2 Uma primitiva para f(x) = 4x3 - 3com(3x) é:
3 A área entre as retas x=e, x=e2, y=0 e a curva y(x) = ln(x) é:
4 Marque a alternativa que corresponde ao valor da integral a seguir:
5 Uma primitiva para é:
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 1 - Encontro 3 /U1S3 - Atividade Diagnóstica
1 A área entre as retas y = 0, x = π e x = 2π e a curva y = sen(x) é:
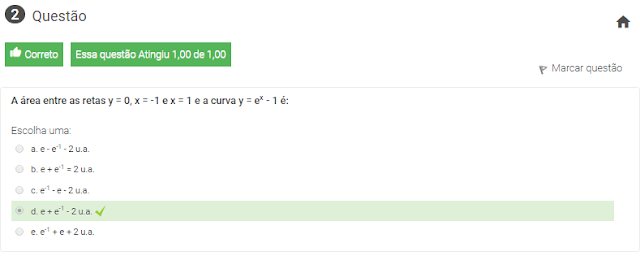
2 A área entre as retas y = 0, x = -1 e x = 1 e a curva y = ex - 1 é:
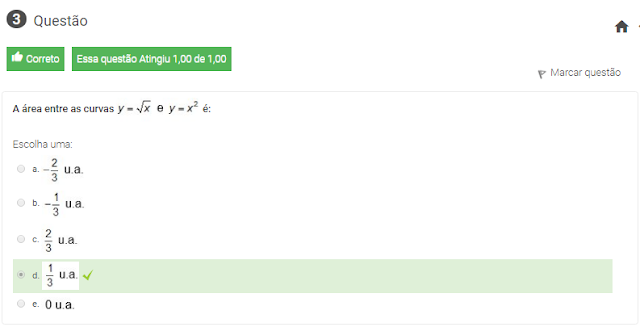
3 A área entre as curvas 
é:
1 A área entre as retas y=0, x=-5, x=3 e a função y(x) = x2 - 36 é
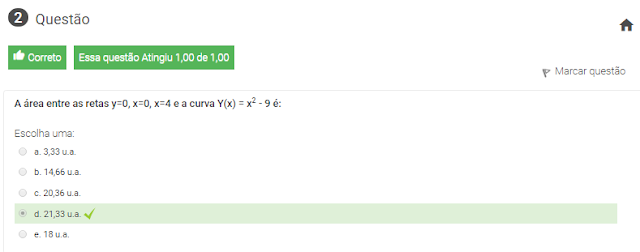
2 A área entre as retas y=0, x=0, x=4 e a curva Y(x) = x2 - 9 é:
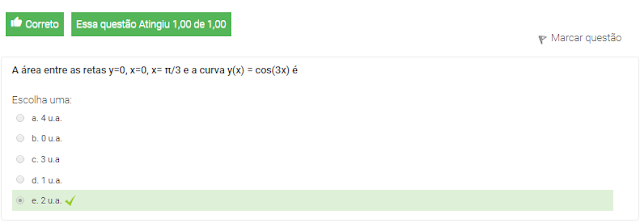
3 A área entre as retas y=0, x=0, x= π/3 e a curva y(x) = cos(3x) é
4 A área entre as curvas y(x) =x2 - 4 e z(x) = x2 - 4 é e é:
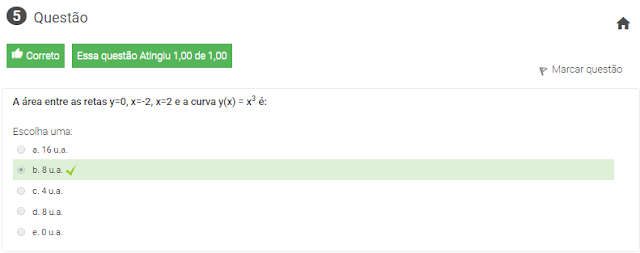
5 A área entre as retas y=0, x=-2, x=2 e a curva y(x) = x3 é:
Segundo tipo de prova
1 A área entre as retas y=0, x=0, x= π/3 e a curva y(x) = cos(3x) é
2 A área entre as retas y=0, x=-5, x=3 e a função y(x) = x2 - 36 é
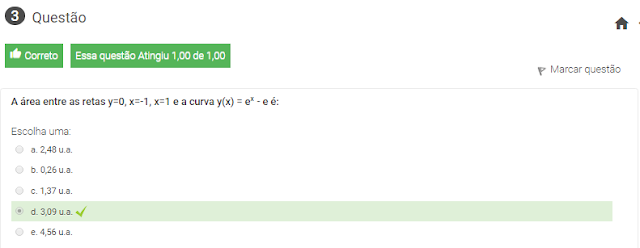
3 A área entre as retas y=0, x=-1, x=1 e a curva y(x) = ex - e é:
4 A área entre as retas y=0, x=1/e , x=1 e a curva y(x) = ln(x) é:
5 A área entre as curvas y(x) =x2 - 4 e z(x) = x2 - 4 é e é:
1 Qual é a função f, cuja derivada é dada por f'(x) = 6x2 - 4x - 3 e f(0) = 5?
2 Um carro inicialmente em repouso acelera a uma taxa a(t) = t3/18. Qual será sua velocidade após 6 segundos?
3 O custo marginal na produção de determinado produto é dado por 
reais por unidade. Atrelando o custo fixo à produção de um único produto, temos c(1) = 555 reais. Determine o custo na produção de 400 produtos?
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 1 - Encontro 4 /U1S4 - Atividade de Aprendizagem
1 Um foguete inicialmente em repouso acelera a uma taxa a(t) = 3t2 (unidade m/s2). Qual será sua velocidade (unidade m/s) após 5 segundos?
2 Uma nave espacial inicialmente em repouso sobre a posição inicial acelera a uma taxa 
(unidade m/s2). Qual será sua posição após 8 segundos?
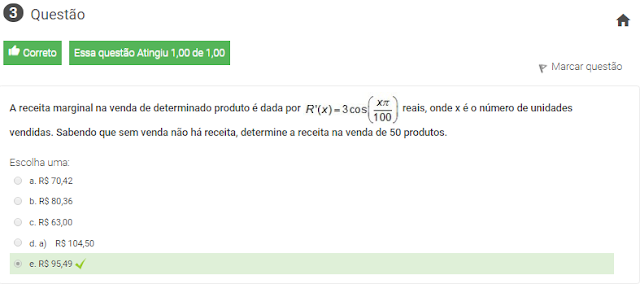
3 A receita marginal na venda de determinado produto é dada por 
reais, onde x é o número de unidades vendidas. Sabendo que sem venda não há receita, determine a receita na venda de 50 produtos.
4 O custo marginal na produção de determinado equipamento é dado por c'(x) = 4/x reais por unidade. Atrelando o custo fixo à produção de um único equipamento, temos c(1)= 450 reais. Determine o custo de 1000 unidades.
5 Qual é a função cuja derivada é dada por f'(x) = 2e2x-3 e f(0) = 1?
Esta questão 5 eu não acertei ela mais acho que a resposta certa é a letra "A" mais eu acho não e certeza quem souber resolver ela mande a resposta nos comentários aki obg :)
Segundo tipo de prova
1 Qual é a função f cuja derivada é dada por f'(x) = ln(2x) e f(1) = 0 e ?
2 Uma nave espacial inicialmente em repouso sobre a posição inicial acelera a uma taxa (unidade m/s2). Qual será sua posição após 8 segundos?
3 Uma certa população de bactérias cresce a uma taxa de 
bactérias por semana. Sabendo que na semana inicial havia duas bactérias, determine o tamanho aproximado da população após 10 semanas.
4 O lucro marginal na venda de determinado produto é dado por L'(x) = 0,03x5 - 0,2x reais por unidade vendida. Sabendo que sem venda não há lucro, determine o lucro para 100 produtos vendidos.
5 Um foguete inicialmente em repouso acelera a uma taxa a(t) = 3t2 (unidade m/s2). Qual será sua velocidade (unidade m/s) após 5 segundos?
Cálculo Diferencial e Integral II /UNIDADE DE ENSINO 1 - Encontro 4 /U1 - Avaliação da Unidade
1 “Determinar as variáveis e as suas relações, talvez seja uma das maiores dificuldades que encontramos ao nos depararmos com problemas do cotidiano.”
Qual é a função , cuja derivada é dada por 
e f(x) = 3?
2 “A técnica de datação por carbono -14 foi descoberta nos anos quarenta, por Willard Libby. Ele percebeu que a quantidade de carbono -14 dos tecidos orgânicos mortos diminuía a um ritmo constante com o passar do tempo. Assim, a medição dos valores de carbono -14 em um objeto antigo nos apresenta pistas muito exatas dos anos decorridos desde sua morte.”
Uma amostra de um certo objeto possui no início do processo de decaimento N(0) = 1x104 núcleos radioativos de carbono-14. Sabendo que a variação do decaimento de núcleos radioativos de carbono-14 com o tempo (em anos) é N(t) = -N(0)λe-λt, em que λ = 1,245x10-0.A alternativa que corresponde ao número de núcleos radioativos após 3000 anos é:
3 “O cálculo de áreas ainda é tema fundamental nas engenharias, seja da área de contato entre vigas (suporte) ou da área de terrenos ou peças. ”
A alternativa que corresponde à área entre as curvas y = 4 e y = x2 é:
4 “Quando analisamos uma empresa para investir (comprar ações), devemos verificar o custo de produção, receita e lucro, entre outros fatores.”
A receita marginal na venda de determinado produto é dada por 
reais por unidade. Sabendo que sem venda não há receita (R(0) = 0) determine a receita na venda de 100 produtos?
5 “Velocidade de internet é um tema bem atual, as operadoras de telefonia celular vivem anunciando sobre a velocidade de seus pacotes.”
No instante em que um cidadão clicou para baixar uma música de 3,3 MB (megabyte), a velocidade do download foi de d'(t) = -0,02t + 0,4 MB/s. Quanto tempo demorou para baixar essa música?
