UNIDADE DE ENSINO 1 - Encontro 1 , U1S1 - Atividade Diagnóstica
1 Dado o gráfico, a lei de formação que representa a função f é:
Escolha uma:
CORRETA É A LETRA 'A'
UNIDADE DE ENSINO 1 - Encontro 1, U1S1 - Atividade de Aprendizagem
UNIDADE DE ENSINO 1 - Encontro 2 / ► U1S2 - Atividade Diagnóstica
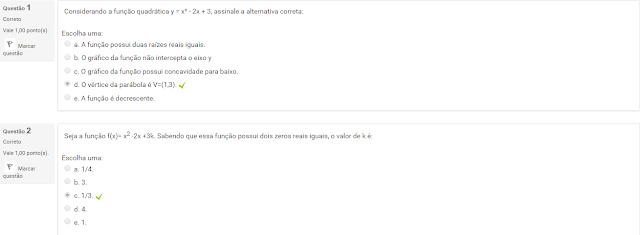
1 Considerando a função quadrática y = x² - 2x + 3, assinale a alternativa correta:
2 Seja a função f(x)= x2 -2x +3k. Sabendo que essa função possui dois zeros reais iguais, o valor de k é:
UNIDADE DE ENSINO 1 - Encontro 2 / ► U1S2 - Atividade de Aprendizagem
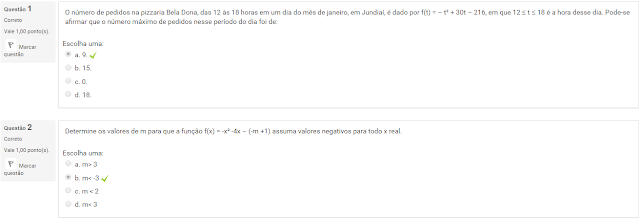
1 O número de pedidos na pizzaria Bela Dona, das 12 às 18 horas em um dia do mês de janeiro, em Jundiaí, é dado por f(t) = – t² + 30t – 216, em que 12 ≤ t ≤ 18 é a hora desse dia. Pode-se afirmar que o número máximo de pedidos nesse período do dia foi de:
2 Determine os valores de m para que a função f(x) = -x² -4x – (-m +1) assuma valores negativos para todo x real.
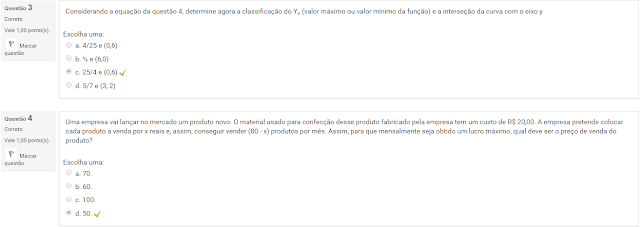
3 Considerando a equação da questão 4, determine agora a classificação do Yv (valor máximo ou valor mínimo da função) e a interseção da curva com o eixo y
4 Uma empresa vai lançar no mercado um produto novo. O material usado para confecção desse produto fabricado pela empresa tem um custo de R$ 20,00. A empresa pretende colocar cada produto à venda por x reais e, assim, conseguir vender (80 - x) produtos por mês. Assim, para que mensalmente seja obtido um lucro máximo, qual deve ser o preço de venda do produto?
UNIDADE DE ENSINO 1 - Encontro 3 / ► U1S3 - Atividade Diagnóstica
1 Considerando a função exponencial y = (1/2) x, assinale a alternativa correta:
2 - A figura a seguir mostra o gráfico da função logaritmo na base b. O valor de b é:
Figura 3 - Gráfico logaritmo
UNIDADE DE ENSINO 1 - Encontro 3 / ► U1S3 - Atividade de Aprendizagem
1 O domínio da função y = log3 (x – ½) é:
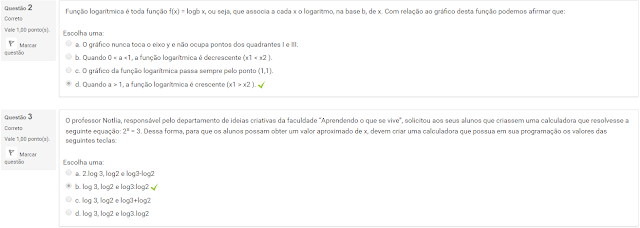
2 Função logarítmica é toda função f(x) = logb x, ou seja, que associa a cada x o logaritmo, na base b, de x. Com relação ao gráfico desta função podemos afirmar que:
3 O professor Notlia, responsável pelo departamento de ideias criativas da faculdade “Aprendendo o que se vive”, solicitou aos seus alunos que criassem uma calculadora que resolvesse a seguinte equação: 2x = 3. Dessa forma, para que os alunos possam obter um valor aproximado de x, devem criar uma calculadora que possua em sua programação os valores das seguintes teclas:
4 Em certo experimento, pesquisadores, ao investigar o desenvolvimento de uma cultura de bactérias, constataram que esta população cresce segundo a expressão N(t) = 768.4t+1 , em que N(t) representa o número de bactérias e t indica o tempo observado em horas. Considerando que foi verificada a existência de um nível crítico, que é quando a cultura atinge 98304 bactérias, qual será o tempo necessário para que o número de bactérias alcance esse nível?
5 Juliana tem duas lojas de roupa A e B, cada uma localizada em um shopping da cidade. O faturamento y de certo produto vendido na loja A pode ser descrito pela função y= 10.3x em que x representa a quantidade de meses desde a inauguração da loja. A loja B vende o dobro da loja A a cada mês. Sabendo que ambas as lojas inauguradas no final de setembro (x=0), em qual final de mês as duas lojas juntas venderam R$ 21870 do produto?
1 Considerando a função trigonométrica f(x)= cosx, assinale a alternativa correta:
1 Considerando a função trigonométrica f(x)= senx, assinale a alternativa correta:
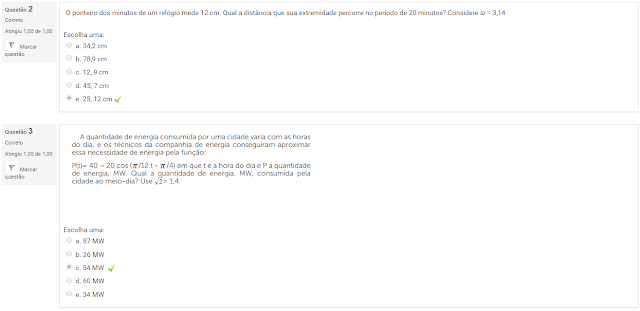
2 O ponteiro dos minutos de um relógio mede 12 cm. Qual a distância que sua extremidade percorre no período de 20 minutos? Considere ϖ = 3,14
3 A quantidade de energia consumida por uma cidade varia com as horas do dia e os técnicos da companhia de energia conseguiram aproximar essa necessidade de
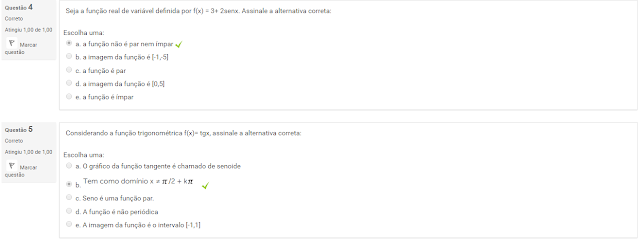
4 Seja a função real de variável definida por f(x) = 3+ 2senx. Assinale a alternativa correta
5 Considerando a função trigonométrica f(x)= tgx, assinale a alternativa correta:
1 Um vendedor recebe mensalmente um salário composto de duas partes: uma parte fixa, no valor de R$ 900,00 e uma variável, que corresponde a uma comissão de 8% do total de vendas que ele fez durante o mês. Qual o salário do vendedor sabendo que durante um mês ele vendeu R$ 50 000,00 em produtos?
2 Um grupo de 100 pessoas fez um contrato com uma empresa aérea para viajar nas férias. A empresa cobrará R$ 2.000,00 por passageiro que embarcar e R$ 400,00 por passageiro que desistir da viagem. Quantos passageiros deverão embarcar para que a empresa receba R$ 136.000?
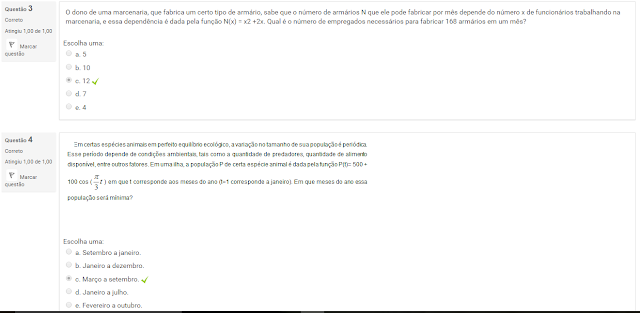
3 O dono de uma marcenaria, que fabrica um certo tipo de armário, sabe que o número de armários N que ele pode fabricar por mês depende do número x de funcionários trabalhando na marcenaria, e essa dependência é dada pela função N(x) = x2 +2x. Qual é o número de empregados necessários para fabricar 168 armários em um mês?
4 Em certas espécies animais em perfeito equilíbrio ecológico,a variação no tamanho de sua população é periódica. Esse período depende de condições