Física Geral e Experimental: Energia /UNIDADE DE ENSINO 1 - Encontro 1 /U1S1 - Atividade Diagnóstica
1 Qual o período do movimento de rotação da terra ao redor de seu próprio eixo? Qual sua frequência de rotação, em rotações por dia? Marque a alternativa com ambas as respostas corretas, respectivamente:
2 O ponteiro dos relógios analógicos realiza um movimento circular uniforme. Calcule a velocidade angular do ponteiro dos minutos na unidade radianos por segundo. Calcule, também, o deslocamento angular do ponteiro dos minutos, se ele sai da marcação 2 e chega à marcação 4. Marque a alternativa com ambas as respostas corretas, respectivamente.
3 Uma betoneira recebe areia, pedras, cimento e água enquanto gira a 30 rpm, produzindo concreto e o mantendo pronto para o uso no momento adequado. Ela tem 1,5m de diâmetro. Marque a opção que possui o período e a velocidade angular do movimento.
Física Geral e Experimental: Energia /UNIDADE DE ENSINO 1 - Encontro 1 /U1S1 - Atividade de Aprendizagem
1 No centro da cidade de Londres existe uma roda gigante muito famosa, chamada “London Eye”.
O visitante pode pagar para dar uma volta completa, que dura 30 minutos.
Qual o deslocamento angular do visitante após de 4 minutos de passeio?
2 Um motor elétrico gira uma pequena esfera presa em um bastão de 1,3 m de comprimento. Dois estudantes decidiram descobrir qual a velocidade angular da esfera. Um possuía um cronômetro e outro fez seu melhor para marcar as posições inicial e final da esfera. Após 5 s no cronômetro, a esfera realizou um arco de circunferência de aproximadamente 3 m. Os estudantes, muito espertos, decidiram que o ponto onde eles iniciaram a medida seria a origem do movimento.
Sabendo disso, qual foi a posição angular final da esfera? E qual a velocidade angular da mesma? Marque a opção com ambas as respostas corretas:
3 Uma partícula executa um movimento circular uniforme de raio 10 centímetros, com uma frequência de 120 rotações por minuto.
O tempo para completar uma volta e sua velocidade linear são respectivamente iguais a:
Física Geral e Experimental: Energia /UNIDADE DE ENSINO 1 - Encontro 2 /U1S2 - Atividade Diagnóstica
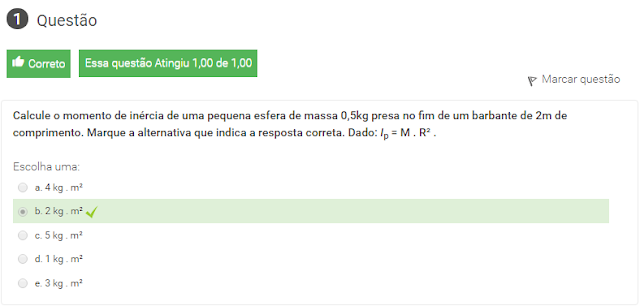
1 Calcule o momento de inércia de uma pequena esfera de massa 0,5kg presa no fim de um barbante de 2m de comprimento. Marque a alternativa que indica a resposta correta. Dado: Ip = M . R² .
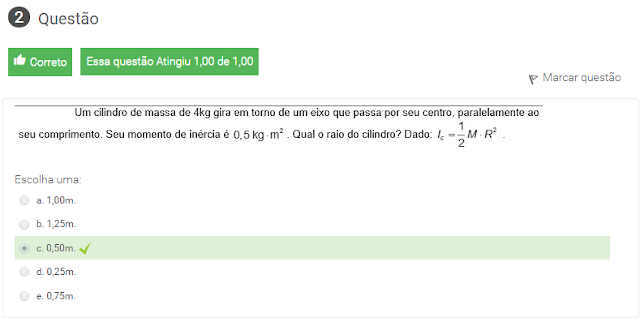
2 Um cilindro de massa de 4kg gira em torno de um eixo que passa por seu centro, paralelamente ao seu comprimento. seu momento de inercia é 0,5 kg.m². qual é o raio do cilindro? dado: Ic = 1/2 M.R²
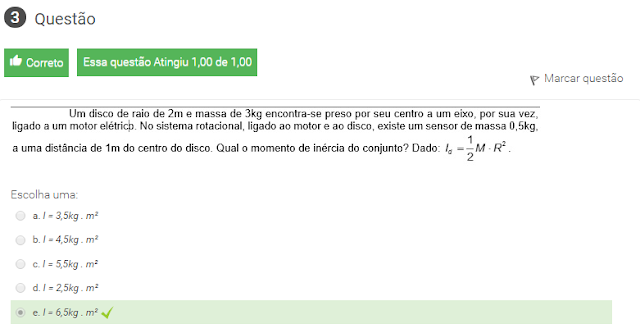
3 Um disco de raio 2m e massa de 3 kg encontra-se preso por seu centro a um eixo, por sua vez, ligado a um motor elétrico. No sistema rotacional, ligado ao motor e ao disco , existe um sensor de massa 0,5 kg, a uma distancia de 1m do centro do disco. Qual o momento de inercia do conjunto? Dado I= 1/2 M.R² Escolha uma: a. I = 5,5kg . m² b. I = 3,5kg . m² c. I = 6,5kg . m² d. I = 4,5kg . m² e. I = 2,5kg . m²
Física Geral e Experimental: Energia /UNIDADE DE ENSINO 1 - Encontro 2 /U1S2 - Atividade de Aprendizagem
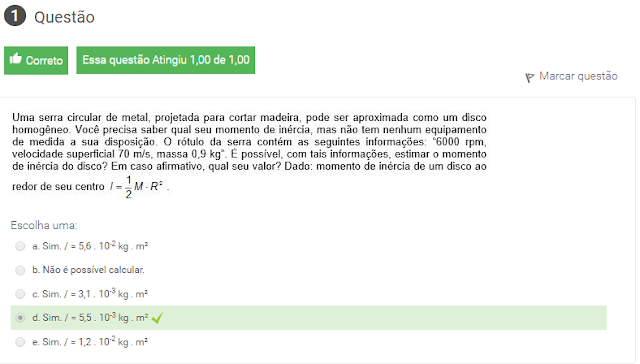
1 Uma serra circular de metal projetada para cortar madeira pode ser aproximada como um disco homogenico voce precisa saber qual seu momento de inercia mas nao tem nenhum equipamento de medida a sua disposicao. o rotulo da serra contem as seguintes informacoes 6000 rpm velocidade superficial 70 m/s massa 0,9 kg. e possivel com tais informacoes estimar o momento de inercia do disco?
2 Duas pequenas esferas de massas m = 2 kg e M = 5 kg giram em torno de um eixo preso em um motor elétrico. Elas estão presas ao eixo por bastões de material muito leve e resistente. A massa m está a uma distância d = 1,5 m e a massa M está a uma distância D = 0,8 m. Qual delas possui o maior momento de inércia? Despreze a contribuição dos bastões. Marque a alternativa que contém a resposta correta e os respectivos momentos de inércia de m e M.
3 O sistema de GPS é um grande feito da engenharia, que transformou uma ideia teórica e aparentemente distante de nossa realidade imediata, a Relatividade de Einstein, em uma indústria multibilionária. Ele funciona com base na comunicação entre diversos satélites, que giram em torno da Terra em órbitas aproximadamente circulares, e um aparelho que deve ser localizado, como, por exemplo, seu smartphone. Os satélites do sistema GPS têm uma massa de 1630 kg e órbitas circulares a uma altura de aproximadamente 20 km da superfície terrestre. Calcule o momento de inércia de um tal satélite. Dado: o raio da Terra é aproximadamente 6370 km.
Física Geral e Experimental: Energia /UNIDADE DE ENSINO 1 - Encontro 3 /U1S3 - Atividade Diagnóstica
1 Com relação à energia, analise as seguintes afirmações.
I- A energia é uma grandeza física escalar que se manifesta de diversas formas. Ela nunca se perde, mas sempre se transforma.
II- A energia é uma abstração matemática que sempre se manifesta da mesma maneira, e ela nunca pode ser transformada, pois não é real.
III- São exemplos de manifestações da energia: energia potencial gravitacional, energia potencial elástica, energia elétrica, energia cinética de translação, energia cinética de rotação.
São corretas as afirmações:
2 Calcule a energia cinética de rotação de uma partícula de massa 0,4kg, que gira livremente com velocidade angular 3,1 rad/s a uma distância de 0,9 m do eixo de rotação. marque a alternativa com a resposta correta, dado:
3 Enunciado: um disco de massa 1,1 kg e raio 0,5 m gira sem atrito em torno de um eixo que passa perpendicularmente ao seu centro, tendo recebido inicialmente uma energia cinética de 4,0 J. Qual sua Frequência de rotação? Dado:
Física Geral e Experimental: Energia /UNIDADE DE ENSINO 1 - Encontro 4 /U1S4 - Atividade Diagnóstica
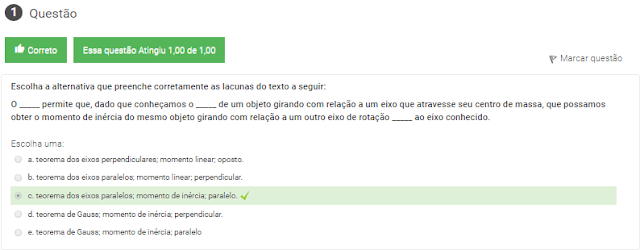
1 Escolha a alternativa que preenche corretamente as lacunas do texto a seguir:
O _____ permite que, dado que conheçamos o _____ de um objeto girando com relação a um eixo que atravesse seu centro de massa, que possamos obter o momento de inércia do mesmo objeto girando com relação a um outro eixo de rotação _____ ao eixo conhecido.
Escolha uma:
2 Um componente eletrônico de 5kg, composto de muitos fios, placas e estrutura metálica foi testado em laboratório e verificou-se que possui um momento de inércia de 45 kg . m² girando com relação a um eixo determinado, que atravessa seu centro de massa. Qual será seu momento de inércia com relação a um outro eixo, paralelo ao primeiro, mas distante em 2m dele?
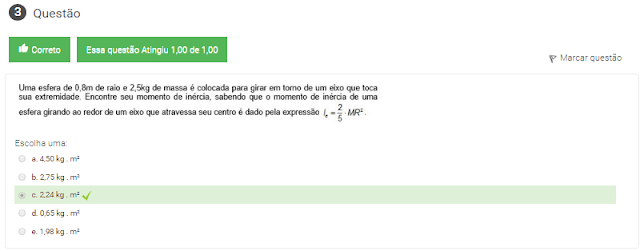
3 Uma esfera de 0,8 m de raio e 2,5 kg de massa é colocada para girar em torno de um eixo que toca sua extremidade. Encontre seu momento de inércia, sabendo que o momento de inércia de uma esfera girando ao redor de um eixo que atravessa seu centro é dado pela expressão: I=2/5*M*R^2.
Física Geral e Experimental: Energia /UNIDADE DE ENSINO 1 - Encontro 3 /U1S3 - Atividade de Aprendizagem
1 Calcule a energia cinetica de um rotor de helicoptero composto por um cilindro central de massa 60kg e raio 50cm, com 4 pás de 4m de comprimento e massa de 180kg cada uma, que gira com frequencia de 300RPM: DAdos momento de inercia de um bastão girando pela extremidade I=1/3.m.L^2; momento de inercia de um cilindro girando em torno do seu eixo de simetria I=1/2.m.r^2;
A resposta certa é1,9x10^6 J
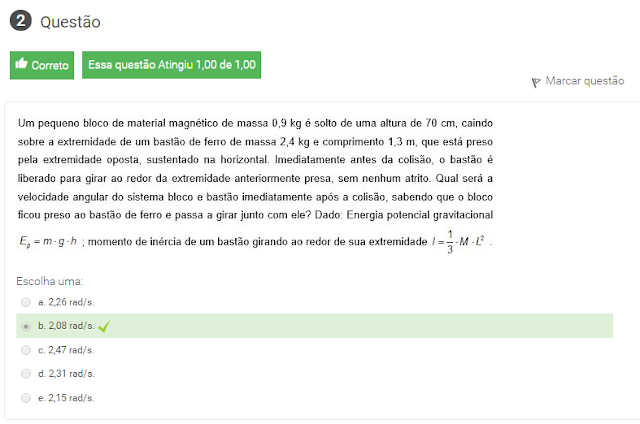
2 Um pequeno bloco de material magnetico de massa 0,9 kg é solto em uma altura de 70 cm, caindo sobre a extremidade de um bastão de massa 2,4 kg e comprimento 1,3 m que esta preso pela extremidade oposta sustentando na horizontal. imediatamente antes da colisão, o bastão e liberado para girar ao redor da extremidade anterior presa, sem nenhum atrito.qual será a velocidade angular do sistema bloco e bastão imediatamente apos a colisão, sabendo que o bloco ficou preso ao bastão de ferro e passa a girar junto com ele?
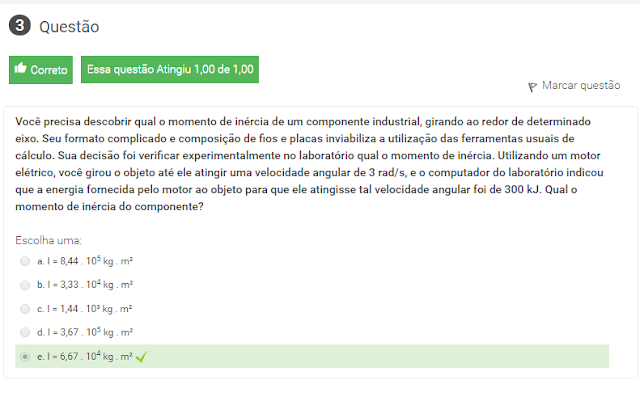
3 Você precisa descobrir qual o momento de inércia de um componente industrial, girando ao redor de determinado eixo. Seu formato complicado e composição de fios e placas inviabiliza a utilização das ferramentas usuais de cálculo. Sua decisão foi verificar experimentalmente no laboratório qual o momento de inércia. Utilizando um motor elétrico, você girou o objeto até ele atingir uma velocidade angular de 3 rad/s, e o computador do laboratório indicou que a energia fornecida pelo motor ao objeto para que ele atingisse tal velocidade angular foi de 300 kJ. Qual o momento de inércia do componente?
outros tipos de questões
2 Uma casca esferica com massa de 1,98 kg e raio 0,44 m é arremessado sobre uma superficie plana. Em determinado momento sua velocidade é medida e verifica-se que o centro de massa se move em linha reta, com velocidade de 5,13 m/s, enquanto que todos os pontos de sua entremidade giram com velocidade angular de 2,75 rad/s em torno de seu eixo central. Calcule sua energia cinetica total. Dado: momento de inercia de uma casca esferica girando em torno de um eixo que atravessa seu centro I = 2/3 . mr².
3 Uma esfera de massa 3,61 kg e raio 0,86m gira sem atrito em torno de um eixo que passa perpendicularmente ao seu centro
Física Geral e Experimental: Energia /UNIDADE DE ENSINO 1 - Encontro 4 /U1S4 - Atividade de Aprendizagem
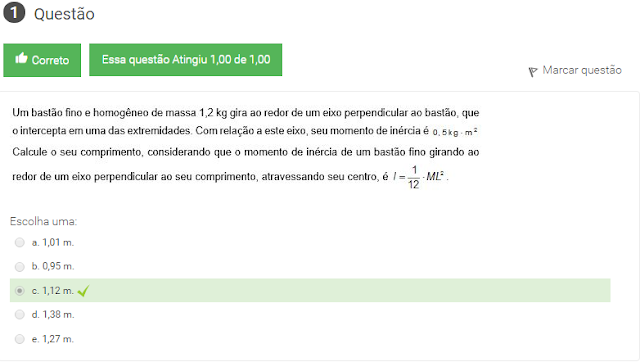
1 Um Bastão fino e homogêneo de massa 1,2 kg gira ao redor de um eixo perpendicular ao batão, que o intercepta em uma extremidades. Com relação a esse eixo, seu momento de inércia é 0,5 kg - m²
Calcule o seu comprimento, considerando que o momento de inércia de um bastão fino girando ao redor de um eixo perpendicular ao seu comprimento, atravessando seu centro, é I=1/12 - ML².
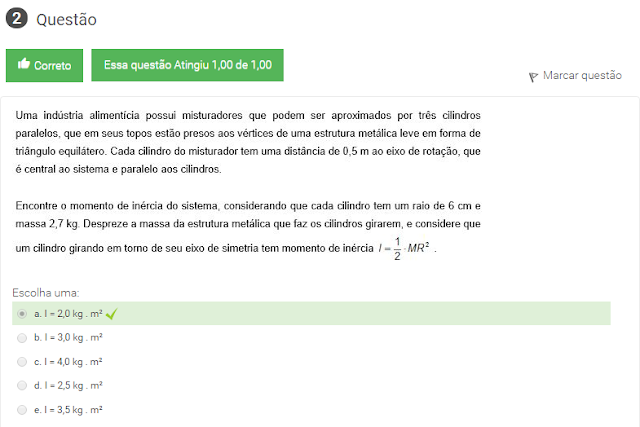
2 Uma Indústria alimentícia possui misturadores que podem ser aproximados por três cilindros paralelos, Que em seus topos estão presos aos vértices de uma estrutura metálica leve em forma de triangulo equilátero. Cada cilindro do misturador tem uma distancia de 0,5 m ao eixo de rotação, que é central ao sistema e paralelos ao cilindros.
Encontre o momento de inércia do sistema, considerando que cada cilindro tem uma raio de 6 cm e massa 2,7 kg. Despreze a massa da estrutura metálica que faz os cilindros girarem , e considere que um cilindro girando em torno de seu eixo de simetria tem momento de inércia I =1/2. MR².
3 Um bastão fino de massa 1,7 kg e 1,5 m de comprimento gira ao redor de um eixo perpendicular ao bastão, que o intercepta a 0,25 m de comprimento de uma de suas extremidade
Calcule o seu momento de inércia, considerando que o momento de inércia de um bastão fino girando ao redor de um eixo perpendicular ao seu comprimento atravessando seu centro é
Física Geral e Experimental: Energia /UNIDADE DE ENSINO 1 - Encontro 4 /U1 - Avaliação da Unidade
1 O movimento circular é extremamente comum na natureza. Qualquer partícula ou corpo rígido que seja obrigado a se mover a uma distância fixa de um eixo de rotação estará realizando um movimento circular. O movimento circular uniforme consiste em um movimento de rotação onde a velocidade angular é constante.
Um motor elétrico gira uma pequena esfera, presa em um bastão de 0,9m de comprimento. Dois estudantes decidiram descobrir qual a velocidade angular da esfera. Um possuía um cronômetro e outro fez seu melhor para marcar as posições inicial e final da esfera. Após 6s no cronômetro, a esfera realizou um arco de circunferência de aproximadamente 2m. Os estudantes, muito espertos, decidiram que o ponto onde eles iniciaram a medida seria a origem do movimento. Sabendo disso, qual foi a posição angular final da esfera? E qual a velocidade angular da mesma? Marque a opção com ambas as respostas corretas:
2 O momento de inércia de corpos rígidos é a soma do momento de inércia de cada uma das pequenas partículas que o compõe. Para corpos mais simétricos, uma boa parametrização e técnicas de integração permitem que o momento de inércia total seja obtido. Para algumas formas simples e comuns, temos expressões tabeladas, que podem ser utilizadas.
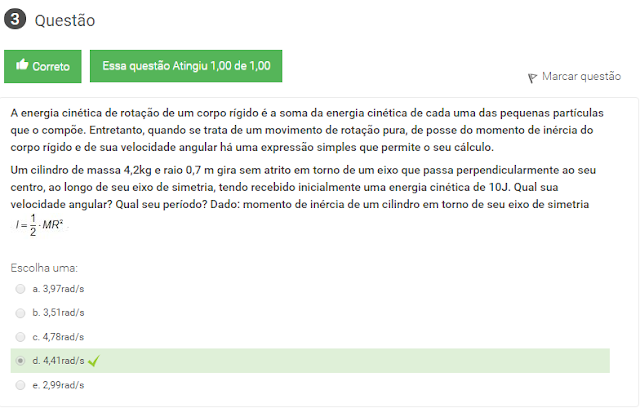
3 A energia cinética de rotação de um corpo rígido é a soma da energia cinética de cada uma das pequenas partículas que o compõe. Entretanto, quando se trata de um movimento de rotação pura, de posse do momento de inércia do corpo rígido e de sua velocidade angular há uma expressão simples que permite o seu cálculo.
Um cilindro de massa 4,2kg e raio 0,7 m gira sem atrito em torno de um eixo que passa perpendicularmente ao seu centro, ao longo de seu eixo de simetria, tendo recebido inicialmente uma energia cinética de 10J. Qual sua velocidade angular? Qual seu período? Dado: momento de inércia de um cilindro em torno de seu eixo de simetria
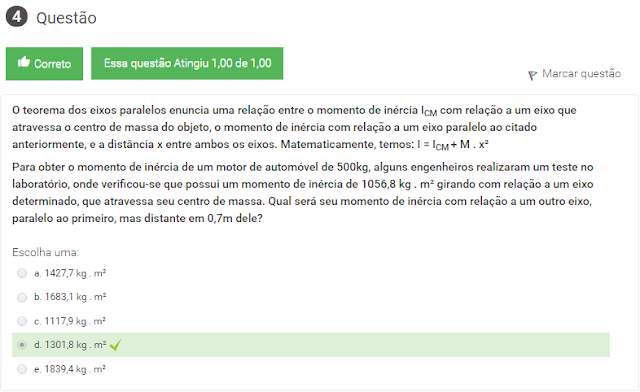
4 O teorema dos eixos paralelos enuncia uma relação entre o momento de inércia ICM com relação a um eixo que atravessa o centro de massa do objeto, o momento de inércia com relação a um eixo paralelo ao citado anteriormente, e a distância x entre ambos os eixos. Matematicamente, temos: I = ICM + M . x²
Para obter o momento de inércia de um motor de automóvel de 500kg, alguns engenheiros realizaram um teste no laboratório, onde verificou-se que possui um momento de inércia de 1056,8 kg . m² girando com relação a um eixo determinado, que atravessa seu centro de massa. Qual será seu momento de inércia com relação a um outro eixo, paralelo ao primeiro, mas distante em 0,7m dele?