Resistência dos Materiais Unidade de ensino 3

Resistência dos Materiais /UNIDADE DE ENSINO 3 - Encontro 1 /U3S1 - Atividade Diagnóstica

 

1 Para um estado de tensão de carregamento multiaxial, devemos expressar as equações a partir das componentes de deformação Ex, Ey e Ez   em função das componentes de tensão  Tx, Ty e Tz. Para isso, teremos que analisar separadamente cada efeito das componentes de tensão e utilizar o princípio de superposição. Este princípio afirma que podemos determinar separadamente os efeitos dos vários carregamentos, que ocorrem de forma combinada, e juntar os resultados obtidos. Para isso, são necessárias duas condições para utilização deste princípio.

Quais condições são necessárias para utilização do princípio de superposição, descrito no texto-base?

Escolha uma:

2 Uma barra, quando submetida a um carregamento de tração axial, além de se alongar no sentido longitudinal a peça irá se contrair lateralmente. O mesmo princípio ocorre quando comprimirmos um material, mudando assim o sentido da força, agora de compressão. Neste caso, a barra tenderá a contrair no sentido longitudinal e expandir no sentido lateral.

Como é conhecida a constante representada pela razão entre a deformação lateral pela deformação longitudinal de um material?

Escolha uma:

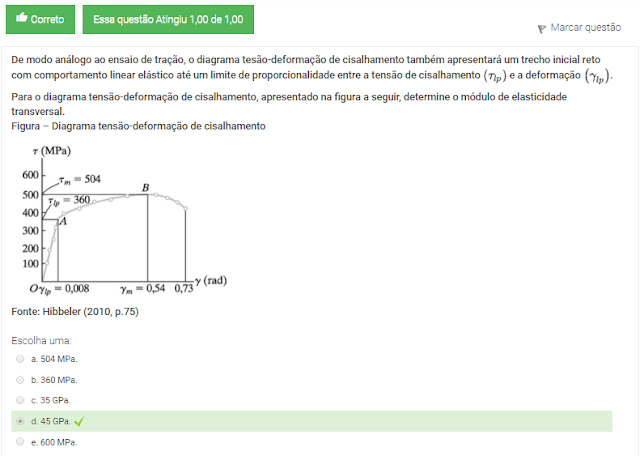
3 De modo análogo ao ensaio de tração, o diagrama tesão-deformação de cisalhamento também apresentará um trecho inicial reto com comportamento linear elástico até um limite de proporcionalidade entre a tensão de cisalhamento(Tlp)  e a deformação (Ylp) .

Para o diagrama tensão-deformação de cisalhamento, apresentado na figura a seguir, determine o módulo de elasticidade transversal.
Figura – Diagrama tensão-deformação de cisalhamento

 

 

Escolha uma:

Resistência dos Materiais /UNIDADE DE ENSINO 3 - Encontro 1 /U3S1 - Atividade de Aprendizagem 

 

1 Tem-se que a generalização da Lei de Hooke ocorre em casos de carregamento multiaxial, sendo que esta lei é válida apenas para materiais com comportamento elástico e o sentido positivo representa tensão de tração e o negativo tensão de compressão.

Uma placa, apresentada na figura a seguir, originalmente tem espessura Ly=25mm  e nela é desenhado um círculo com diâmetro de 200mm . Sabendo que as tensões aplicadas tem intensidade de tx=90MPa e tz=150MPa  e o material tem um coeficiente Poisson v=0,30  e um módulo de elasticidade E=100GPa, deseja-se saber qual o comprimento em AB , o comprimento em CD  e a espessura da placa após a aplicação das tensões.
Figura – Desenho esquemático da placa

 

 

Escolha uma:

 

2 De modo análogo ao ensaio de tração, o diagrama tesão-deformação de cisalhamento também apresentará um trecho inicial reto com comportamento linear elástico até um limite de proporcionalidade entre a tensão de cisalhamento (Tlp) e a deformação (Ylp).

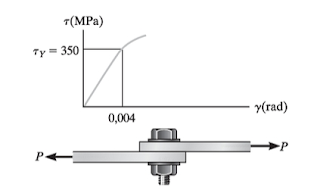
A partir do diagrama tensão-deformação de cisalhamento do material do elemento de ligação apresentado na figura, determine o módulo de elasticidade e o carregamento P necessário para provocar o escoamento do material. Sabendo que o parafuso tem diâmetro de 5 mm e coeficiente de Poisson é igual a 0,35.
Figura – Diagrama tensão-deformação de cisalhamento.

 

Escolha uma:

3 A distorção do ângulo interno de uma peça é conhecida como deformação de cisalhamento, representada pela letra grega Y, e expressa em radianos. As letras subscritas são correspondentes as direções nas quais ocorrem a mudança do ângulo. Estas propriedades podem ser medidas em ensaios de laboratório para constatação do comportamento do material.

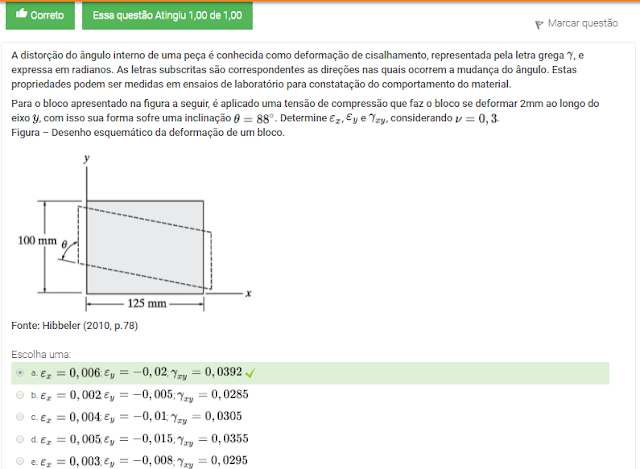
Para o bloco apresentado na figura a seguir, é aplicado uma tensão de compressão que faz o bloco se deformar 2mm ao longo do eixo y, com isso sua forma sofre uma inclinação 0=88º . Determine Ex, Ey e Yxy , considerando v=0,3 .
Figura – Desenho esquemático da deformação de um bloco.

Escolha uma:

 Resistência dos Materiais /UNIDADE DE ENSINO 3 - Encontro 2 /U3S2 - Atividade Diagnóstica

 

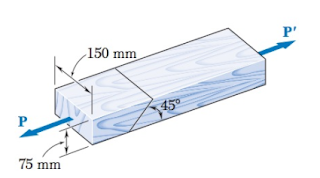
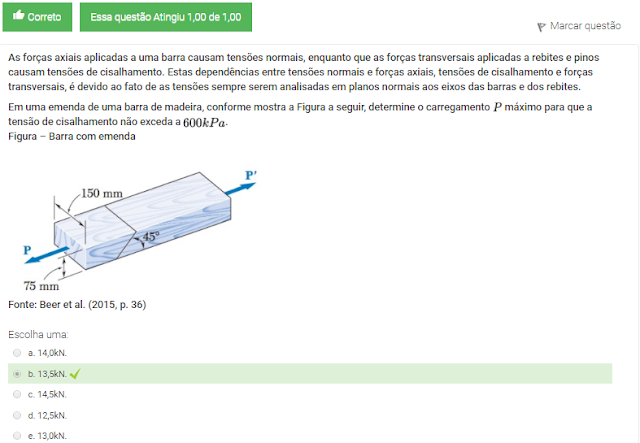
1 As forças axiais aplicadas a uma barra causam tensões normais, enquanto que as forças transversais aplicadas a rebites e pinos causam tensões de cisalhamento. Estas dependências entre tensões normais e forças axiais, tensões de cisalhamento e forças transversais, é devido ao fato de as tensões sempre serem analisadas em planos normais aos eixos das barras e dos rebites.

Em uma emenda de uma barra de madeira, conforme mostra a Figura a seguir, determine o carregamento P máximo para que a tensão de cisalhamento não exceda a 600KPa.
Figura – Barra com emenda

Fonte: Beer et al. (2015, p. 36)

Escolha uma:

2 “Vimos que forças axiais aplicadas em um elemento de barra provocavam tensões normais na barra, enquanto forças transversais agindo sobre parafusos e pinos provocavam tensões de cisalhamento nas conexões. A razão pela qual se observou uma relação entre forças axiais e tensões normais, por um lado, e forças transversais e tensões de cisalhamento, por outro lado, era porque as tensões estavam sendo determinadas apenas em planos perpendiculares ao eixo do elemento ou conexão. ”

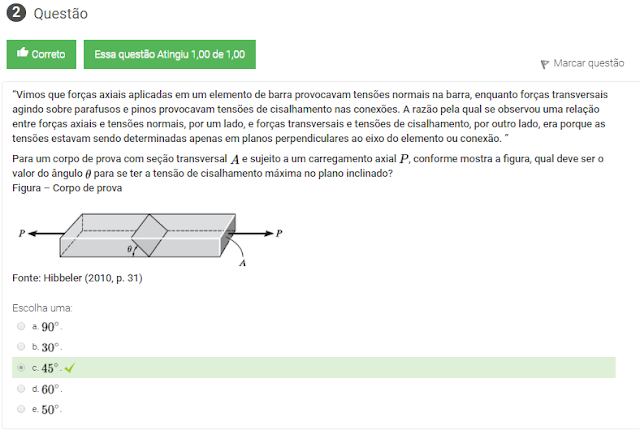
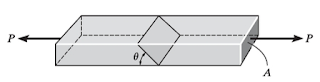
Para um corpo de prova com seção transversal A e sujeito a um carregamento axial P, conforme mostra a figura, qual deve ser o valor do ângulo para se ter a tensão de cisalhamento máxima no plano inclinado?
Figura – Corpo de prova

Fonte: Hibbeler (2010, p. 31)

Escolha uma:

3 Para melhorar o entendimento do estado de tensão do ponto Q no material, vamos analisar um cubo de lado a com centro no ponto Q, com as tensões aplicadas em cada face do cubo, conforme mostra a Figura a seguir. Nas faces visíveis na Figura, temos as tensões normais Tx, Ty e Tz aplicadas às faces perpendiculares aos eixos x, y e z, respectivamente, e as seis tensões de cisalhamento Txy, Txz, Tyx, Tyz, Tzx e Tzy. Nas faces não visíveis na Figura as tensões têm o mesmo módulo com sentidos opostos.
Figura – Estado de tensões.

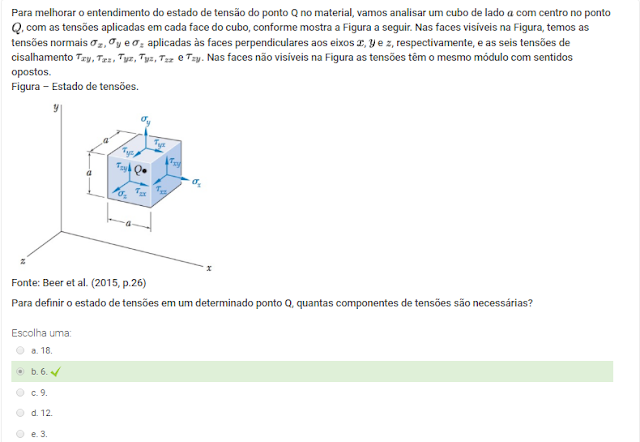
Fonte: Beer et al. (2015, p.26)

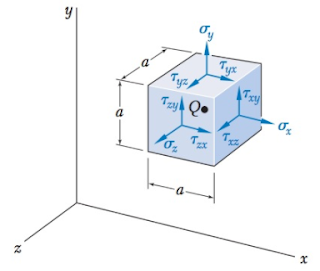
Para definir o estado de tensões em um determinado ponto Q, quantas componentes de tensões são necessárias?

Escolha uma:

 Resistência dos Materiais /UNIDADE DE ENSINO 3 - Encontro 2 /U3S2 - Atividade de Aprendizagem

 

1 Um carregamento axial pode causar tensões normais e cisalhantes desde que o plano de aplicação do carregamento e o carregamento não sejam perpendiculares entre si. Da mesma forma, os esforços cortantes atuantes na seção transversal de um parafuso podem causar tensões normais e cisalhantes, atuantes em cada um dos infinitos planos não perpendiculares ao eixo do parafuso.

Para uma emenda de uma barra de madeira, mostrada na Figura a seguir, determine a tensão normal e a tensão de cisalhamento na emenda, sabendo que o carregamento é P=8KN.
Figura – Barra com emenda.

 

Fonte: Beer et al. (2015, p.36)

Escolha uma:

2 Para tensões em um plano obliquo ao eixo, quando o plano inclinado tem um ângulo =0, tem-se uma tensão normal máxima (Tm=P/A0) . Por outro lado, a tensão tende a zero quando o ângulo TETA se aproxima de 90º. A tensão de cisalhamento é nula quando TETA =0 e TETA=90º. Porém para TETA=45º, tem-se a máxima tensão de cisalhamento.

Determine a tensão normal e a de cisalhamento para o plano obliquo apresentado na Figura a seguir.
Figura – Tensão em um plano obliquo

Fonte: Hibbeler (2010, p. 31)

Escolha uma:

3 “Vimos que forças axiais aplicadas em um elemento de barra provocavam tensões normais na barra, enquanto forças transversais agindo sobre parafusos e pinos provocavam tensões de cisalhamento nas conexões. A razão pela qual se observou uma relação entre forças axiais e tensões normais, por um lado, e forças transversais e tensões de cisalhamento, por outro lado, era porque as tensões estavam sendo determinadas apenas em planos perpendiculares ao eixo do elemento ou conexão. ”

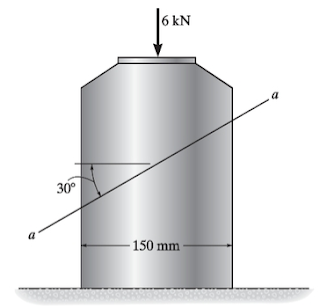
Em um bloco de apoio quadrado com lado medindo 150mm, conforme mostrado na Figura, temos um carregamento de 6KN. Determine a tensão normal e de cisalhamento na seção a-a. 
Figura – Bloco de apoio

Fonte: Hibbeler (2010, p.45)

Escolha uma:

 Resistência dos Materiais /UNIDADE DE ENSINO 3 - Encontro 3 /U3S3 - Atividade Diagnóstica

 

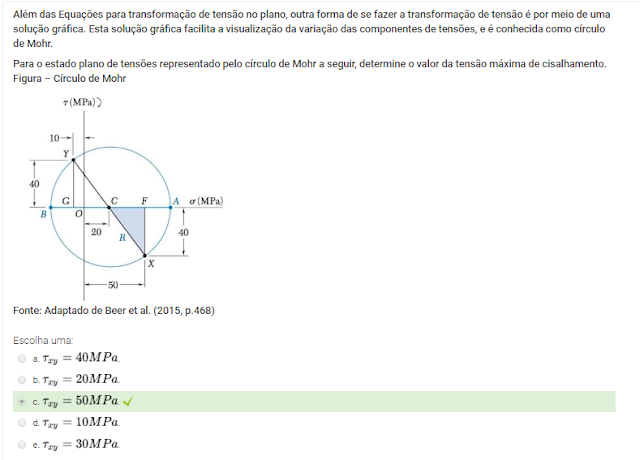
1 Além das Equações para transformação de tensão no plano, outra forma de se fazer a transformação de tensão é por meio de uma solução gráfica. Esta solução gráfica facilita a visualização da variação das componentes de tensões, e é conhecida como círculo de Mohr.

Para o estado plano de tensões representado pelo círculo de Mohr a seguir, determine o valor da tensão máxima de cisalhamento.
Figura – Círculo de Mohr

Fonte: Adaptado de Beer et al. (2015, p.468)

Escolha uma:

2 Na prática profissional, é comum a busca pela direção em que ocorrerão as máximas tensões no plano. Para isso, a fim de se determinar a tensão normal máxima e mínima devemos derivar a Equação das componentes de tensão em relação ao ângulo do plano inclinado e igualar a zero. Temos, assim, a Equação das tensões principais.

Para o círculo de Mohr apresentado na figura, identifique as tensões principais.
Figura – Círculo de Mohr

Fonte: Beer et al. (2015, p. 469)

Escolha uma:

3 O estado geral de tensão em um ponto é determinado por seis componentes, três componentes de tensão normal e outras três componentes de tensão de cisalhamento. Este estado de tensão, na prática profissional, para facilitar a interpretação dos problemas reais, é simplificado a um estado plano de tensão.

Para o estado plano de tensão apresentado na Figura, identifique quais as tensões atuantes, sabendo que trata-se de um plano x-y.    

Figura – Estado plano de tensão

Fonte: Adaptado de Hibbeler (2010, p.333)

Escolha uma:

 Resistência dos Materiais /UNIDADE DE ENSINO 3 - Encontro 3 /U3S3 - Atividade de Aprendizagem

 

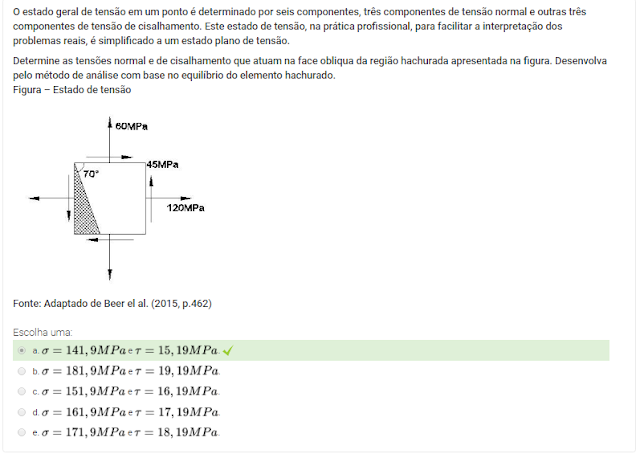
1 O estado geral de tensão em um ponto é determinado por seis componentes, três componentes de tensão normal e outras três componentes de tensão de cisalhamento. Este estado de tensão, na prática profissional, para facilitar a interpretação dos problemas reais, é simplificado a um estado plano de tensão.

Determine as tensões normal e de cisalhamento que atuam na face obliqua da região hachurada apresentada na figura. Desenvolva pelo método de análise com base no equilíbrio do elemento hachurado.
Figura – Estado de tensão

Fonte: Adaptado de Beer el al. (2015, p.462)

Escolha uma:

2 Na prática profissional é comum a busca pela direção em que ocorrerão as máximas tensões no plano. Com isso, para se determinar a tensão normal máxima e mínima, devemos derivar a Equação das componentes de tensão em relação ao ângulo do plano inclinado e igualando a zero. Assim, temos as Equações das tensões principais.

Determine as tensões principais para o estado de tensão apresentado na Figura.
Figura – Estado de tensão

Fonte: Beer el al. (2015, p.462)

Escolha uma:

3 “O estado de tensão no ponto também pode ser representado como a tensão de cisalhamento máxima no plano. Nesse caso, uma tensão normal média também age no elemento.

Os planos para tensão de cisalhamento máxima podem ser determinados orientando um elemento a 45º em relação à posição de um elemento que define os planos das tensões principais”.

Determine a tensão máxima de cisalhamento e a orientação deste plano para o estado de tensão apresentado na Figura.
Figura – Estado de tensão

Fonte: Adaptado de Beer el al. (2015, p.462)

Escolha uma:

 Resistência dos Materiais /UNIDADE DE ENSINO 3 - Encontro 3 /U3 - Avaliação da Unidade

 

1 Tem-se que a generalização da Lei de Hooke ocorre em casos de carregamento multiaxial, sendo que esta lei é válida apenas para materiais com comportamento elástico. O sentido positivo da tensão representa uma tensão de tração e o sentido negativo da tensão, representa uma tensão de compressão.

Em uma placa com dimensões apresentadas na figura a seguir e espesssura de 5 mm, foi desenhado uma linha com inclinação 4:10. Sabendo que E=100GPa  e v=0,30, determine a inclinação da linha após ocorrer a deformação devido ao carregamento apresentado na figura.
Figura - Desenho esquemático da placa

Fonte: Beer el al. (2015, p. 103)

Escolha uma:

2 Um carregamento axial pode causar tensões normais e cisalhantes, desde que o plano de aplicação do carregamento e o carregamento não sejam perpendiculares entre si. Da mesma forma, os esforços cortantes atuantes na seção transversal de um parafuso podem causar tensões normal e cisalhante, atuantes em cada um dos infinitos planos não perpendiculares ao eixo do parafuso.

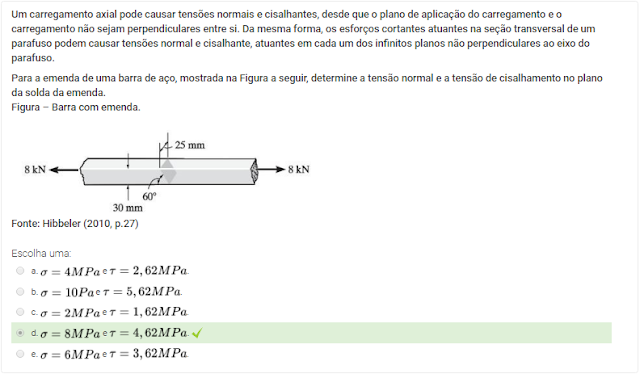
Para a emenda de uma barra de aço, mostrada na Figura a seguir, determine a tensão normal e a tensão de cisalhamento no plano da solda da emenda.
Figura – Barra com emenda.

Fonte: Hibbeler (2010, p.27)

Escolha uma:

3 “Vimos que forças axiais aplicadas em um elemento de barra provocavam tensões normais na barra, enquanto forças transversais agindo sobre parafusos e pinos provocavam tensões de cisalhamento nas conexões. A razão pela qual se observou uma relação entre forças axiais e tensões normais, por um lado, e forças transversais e tensões de cisalhamento, por outro lado, era porque as tensões estavam sendo determinadas apenas em planos perpendiculares ao eixo do elemento ou conexão”.

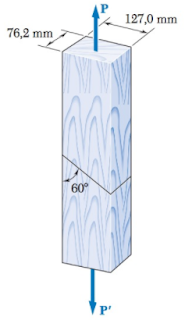
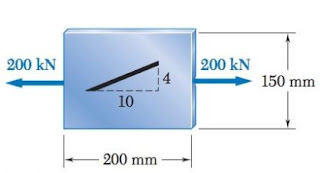
Em um ensaio de tração, um corpo de prova de aço rompeu-se a um ângulo de 52º, conforme mostra a figura a seguir. Sabendo que o diâmetro do corpo de prova é de 12mm e a carga de ruptura foi de 200Kn, determine a tensão normal e a tensão de cisalhamento que ocorreu na área do plano de ruptura inclinado.
Figura – Corpo de prova de aço

Fonte: Hibbeler (2010, p. 28)

Escolha uma:

4 O estado geral de tensão em um ponto é determinado por seis componentes: três componentes de tensão normal e outras três componentes de tensão de cisalhamento. Este estado tridimensional de tensão, na prática profissional, para facilitar a interpretação dos problemas reais, é simplificado a um estado plano de tensão.

Determine as tensões normal e de cisalhamento que atuam na face obliqua da região sombreada apresentada na figura a seguir. Desenvolva as equações aplicando o equilíbrio de forças atuantes no elemento sombreado.
Figura – Estado plano de tensão

Fonte: Beer et al. (2015, p. 462)

Escolha uma:

5 Na prática profissional, é comum a busca pela direção onde ocorrerão as máximas tensões no plano. Com isso, para se determinar a tensão normal máxima e mínima, devemos derivar a equação das componentes de tensão em relação ao ângulo do plano inclinado e igualar a zero. Assim, temos a equação das tensões principais.

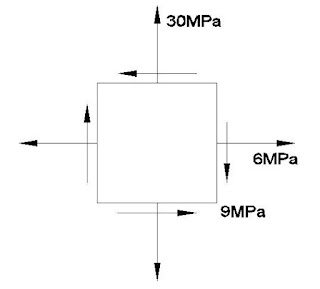
Determine as tensões principais para o estado de tensão apresentado na Figura.
Figura – Estado plano de tensão

Fonte: Beer el al. (2015, p.462)

Escolha uma: