Resistência dos Materiais /UNIDADE DE ENSINO 2 - Encontro 1 /U2S1 - Atividade Diagnóstica
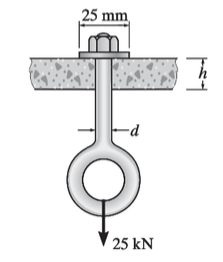
1 As tensões utilizadas para o dimensionamento dos elementos estruturais são as tensões admissíveis (adm), ou seja, é admissível por questão de segurança não expor o projeto às condições de ruptura, uma vez que a estrutura em utilização pode apresentar outros carregamentos além do considerado em projeto.
Calcule o diâmetro do parafuso para o carregamento de 25 kN, conforme apresentado na figura. Sabendo que a tensão normal de ruptura do material é de 600 MPa e o coeficiente de segurança igual a 3. Obtenha o diâmetro múltiplo de 0,5 mm.
Figura - Parafuso
Escolha uma:
2 “ Para se garantir a segurança, é preciso escolher uma tensão admissível que restrinja a carga aplicada a um valor menor do que a carga que o elemento pode suportar totalmente. Há várias razões para isso. Por exemplo, a carga para a qual o elemento é projetado pode ser diferente das cargas realmente aplicadas.”
Para uma barra quadrada que possui uma carga de ruptura de tração P igual a 30kN, conforme apresentado na figura, calcule a medida do lado da seção transversal da barra de projeto sabendo que o material possui u=300MPa e adm=100MPa .
Figura - Barra
Escolha uma:
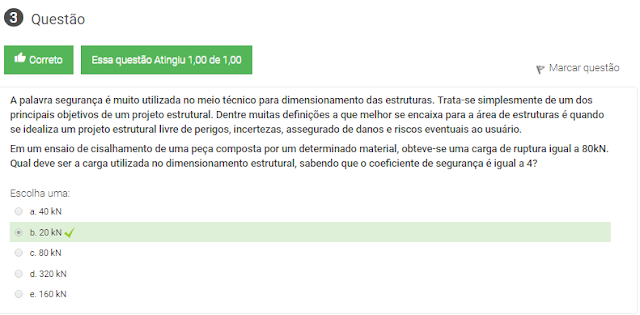
3 A palavra segurança é muito utilizada no meio técnico para dimensionamento das estruturas. Trata-se simplesmente de um dos principais objetivos de um projeto estrutural. Dentre muitas definições a que melhor se encaixa para a área de estruturas é quando se idealiza um projeto estrutural livre de perigos, incertezas, assegurado de danos e riscos eventuais ao usuário.
Em um ensaio de cisalhamento de uma peça composta por um determinado material, obteve-se uma carga de ruptura igual a 80kN. Qual deve ser a carga utilizada no dimensionamento estrutural, sabendo que o coeficiente de segurança é igual a 4?
Escolha uma:
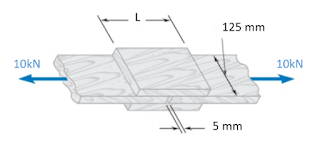
1 A tensão última (u), como o nome já diz, é relativa a máxima tensão que atua em uma peça antes dela se romper. Pode ter obtida a partir da força última (Pu), esta força é o máximo carregamento até a ruptura do material. Para se conhecer estas forças e tensões para cada material, normalmente iremos obtê-las por meio de ensaios em laboratórios ou em campo, ensaios estes que têm como objetivo simular as condições de carregamento de utilização até a ruptura do material.
Para um ensaio de cisalhamento, duas barras de madeira suportam uma carga de 10kN e estão conectadas por duas chapas, de comprimento L, perfeitamente coladas nas barras, conforme figura. Sabe-se que a tensão de cisalhamento último da cola é de 3MPa e o espaçamento entre as barras é de 5mm. Determine o comprimento L de ruptura para que a conexão trabalhe com coeficiente de segurança igual a 3.
Figura – Ensaio de Cisalhamento.
Fonte: Adaptado de Beer et al. (2015, p.38).
Escolha uma:
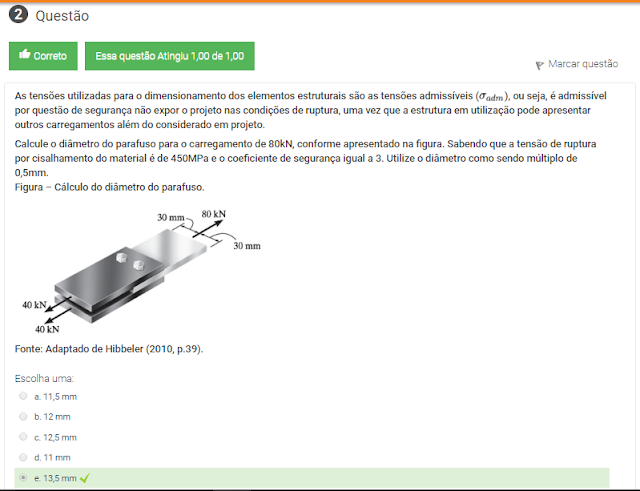
2 As tensões utilizadas para o dimensionamento dos elementos estruturais são as tensões admissíveis (adm), ou seja, é admissível por questão de segurança não expor o projeto nas condições de ruptura, uma vez que a estrutura em utilização pode apresentar outros carregamentos além do considerado em projeto.
Calcule o diâmetro do parafuso para o carregamento de 80kN, conforme apresentado na figura. Sabendo que a tensão de ruptura por cisalhamento do material é de 450MPa e o coeficiente de segurança igual a 3. Utilize o diâmetro como sendo múltiplo de 0,5mm.
Figura – Cálculo do diâmetro do parafuso.
Fonte: Adaptado de Hibbeler (2010, p.39).
Escolha uma:
3 A escolha do coeficiente de segurança (CS) trata de um dos mais importantes problemas técnicos. Um CS baixo pode colocar em risco o projeto, perdendo o sentido da segurança, por outro lado, um alto CS pode elevar demais os custos do projeto inviabilizando economicamente.
Determine o diâmetro das hastes AB e CD que suportam a viga AC, conforme figura, utilizando um coeficiente de segurança igual a 2. Sabe-se que a tensão de ruptura do material das barras é de 400 MPa.
Figura – Cálculo do diâmetro das hastes.
Fonte: Adaptado de Hibbeler (2010, p.39).
1 O diagrama tensão-deformação pode variar muito de um material para outro, dependendo das características mecânicas de cada material. Uma interpretação importante deste diagrama é a possibilidade em identificar grupos de materiais.
Quais grupos de materiais podem ser identificados, a partir da interpretação do diagrama tensão-deformação?
Para uma barra de aço dúctil, qual o nome do fenômeno que ocorre após a tensão última durante um ensaio de tração?
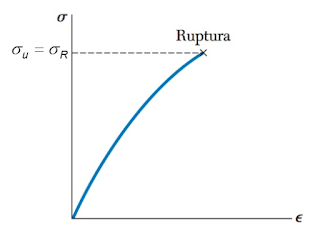
Analisando diagrama tensão-deformação apresentado na Figura a seguir, pode-se identificar que se trata de um material:
Figura – Diagrama tensão-deformação
Fonte: Adaptado de Beer et a. (2015, p.55).
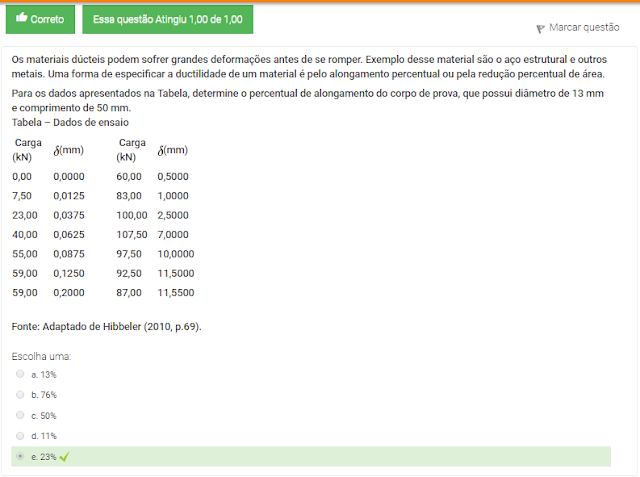
1 Os materiais dúcteis podem sofrer grandes deformações antes de se romper. Exemplo desse material são o aço estrutural e outros metais. Uma forma de especificar a ductilidade de um material é pelo alongamento percentual ou pela redução percentual de área.
Para os dados apresentados na Tabela, determine o percentual de alongamento do corpo de prova, que possui diâmetro de 13 mm e comprimento de 50 mm.
Tabela – Dados de ensaio
|
Carga (kN) |
(mm) |
|
Carga (kN) |
(mm) |
|
0,00 |
0,0000 |
60,00 |
0,5000 |
|
|
7,50 |
0,0125 |
83,00 |
1,0000 |
|
|
23,00 |
0,0375 |
100,00 |
2,5000 |
|
|
40,00 |
0,0625 |
107,50 |
7,0000 |
|
|
55,00 |
0,0875 |
97,50 |
10,0000 |
|
|
59,00 |
0,1250 |
92,50 |
11,5000 |
|
|
59,00 |
0,2000 |
87,00 |
11,5500 |
Fonte: Adaptado de Hibbeler (2010, p.69).
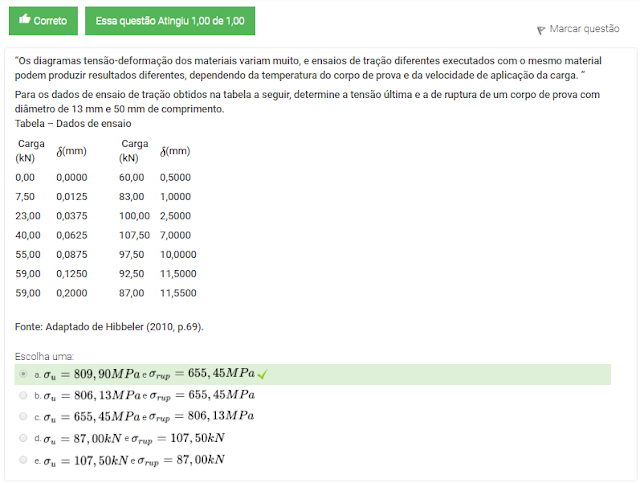
Para os dados de ensaio de tração obtidos na tabela a seguir, determine a tensão última e a de ruptura de um corpo de prova com diâmetro de 13 mm e 50 mm de comprimento.
Tabela – Dados de ensaio
|
Carga (kN) |
(mm) |
|
Carga (kN) |
(mm) |
|
0,00 |
0,0000 |
60,00 |
0,5000 |
|
|
7,50 |
0,0125 |
83,00 |
1,0000 |
|
|
23,00 |
0,0375 |
100,00 |
2,5000 |
|
|
40,00 |
0,0625 |
107,50 |
7,0000 |
|
|
55,00 |
0,0875 |
97,50 |
10,0000 |
|
|
59,00 |
0,1250 |
92,50 |
11,5000 |
|
|
59,00 |
0,2000 |
87,00 |
11,5500 |
Fonte: Adaptado de Hibbeler (2010, p.69).
Desenhe o diagrama tensão-deformação com os dados da Tabela a seguir e identifique qual é o tipo de material do corpo de prova.
Tabela – Dados de ensaio
|
(MPa) |
(mm/mm |
|
0,0 |
0,0000 |
|
232,4 |
0,0006 |
|
318,5 |
0,0010 |
|
345,8 |
0,0014 |
|
360,5 |
0,0018 |
|
373,8 |
0,0022 |
Fonte: Adaptado Hibbeler (2010, p. 68)
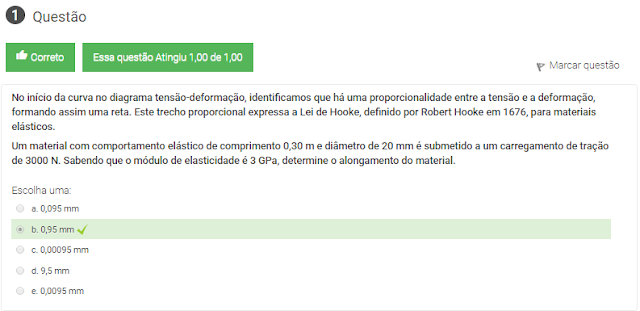
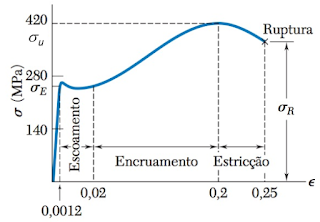
1 No início da curva no diagrama tensão-deformação, identificamos que há uma proporcionalidade entre a tensão e a deformação, formando assim uma reta. Este trecho proporcional expressa a Lei de Hooke, definido por Robert Hooke em 1676, para materiais elásticos.
Um material com comportamento elástico de comprimento 0,30 m e diâmetro de 20 mm é submetido a um carregamento de tração de 3000 N. Sabendo que o módulo de elasticidade é 3 GPa, determine o alongamento do material.
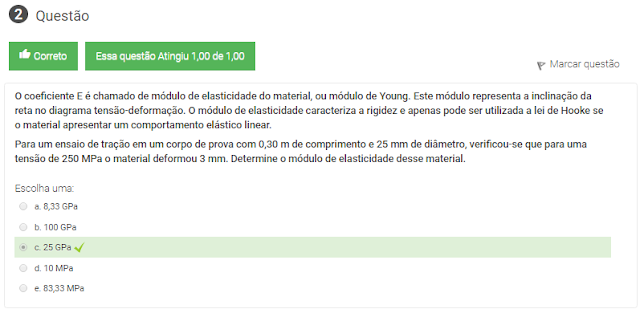
Para um ensaio de tração em um corpo de prova com 0,30 m de comprimento e 25 mm de diâmetro, verificou-se que para uma tensão de 250 MPa o material deformou 3 mm. Determine o módulo de elasticidade desse material.
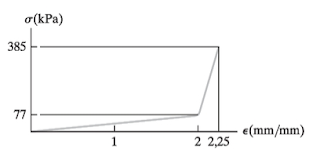
Determine o módulo de elasticidade do material, utilizando as informações contidas no diagrama tensão-deformação do material, mostradas na figura.
Figura – Diagrama tensão-deformação.
Escolha uma:
Resistência dos Materiais /UNIDADE DE ENSINO 2 - Encontro 3 /U2S3 - Atividade de Aprendizagem
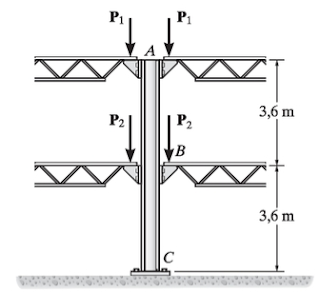
1 Em uma edificação, os pilares são elementos estruturais, conhecidos popularmente como colunas, que transmitem as cargas do edifício para a fundação. Este carregamento é aplicado no sentido da força peso, ou seja, verticalmente, e distribuído na fundação, gerando uma tensão normal de compressão.
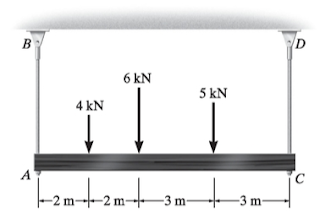
Determine o deslocamento no topo do pilar A apresentado na figura, para um pilar quadrado de seção de 0,20m por 0,20m e carregamento P1=250KN e P2=300KN, com E=250GPa .
Figura –Desenho esquemático do pilar.
Fonte: Hibbeler (2010, p. 91).
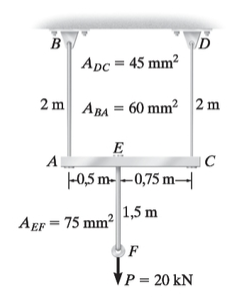
Para o suporte apresentado na Figura, determine o deslocamento vertical do ponto F, sabendo que as barras AB, CD e EF são deformáveis e têm E=400GPa , e a barra AC trata-se de uma barra indeformável.
Figura – Desenho esquemático do suporte.
Fonte: Hibbeler (2010, p. 93).
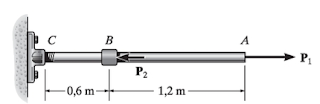
Calcule a deformação da barra apresentada na figura. Considere: P1=100KN, P2=70KN, diâmetro dos dois trecho de 20mm, Ebc=200GPa e Eab=100GPa .
Figura - Barra
Fonte: Hibbeler (2010, p. 92).
Resistência dos Materiais /UNIDADE DE ENSINO 2 - Encontro 3 /U2 - Avaliação da Unidade
1 As tensões utilizadas para o dimensionamento dos elementos estruturais são as tensões admissíveis (). Desta maneira, é admissível, por questão de segurança, não expor o projeto nas condições de ruptura, uma vez que a estrutura em utilização pode apresentar outros carregamentos, além do carregamento considerado em projeto.
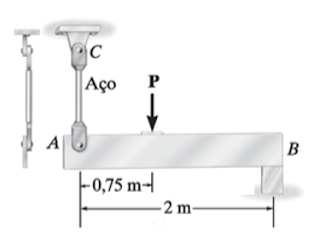
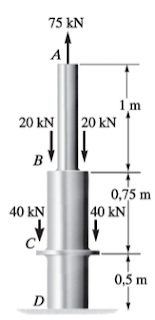
A barra rígida AB mostrada na figura é sustentada por uma haste redonda de aço. Determine o diâmetro da haste, sabendo a tensão última do aço é 680MPa, o coeficiente de segurança CS=2 e o carregamento P=200KN.
Figura - Desenho esquemático do suporte de aço
Fonte: Adaptado Hibbeler (2010, p.38)
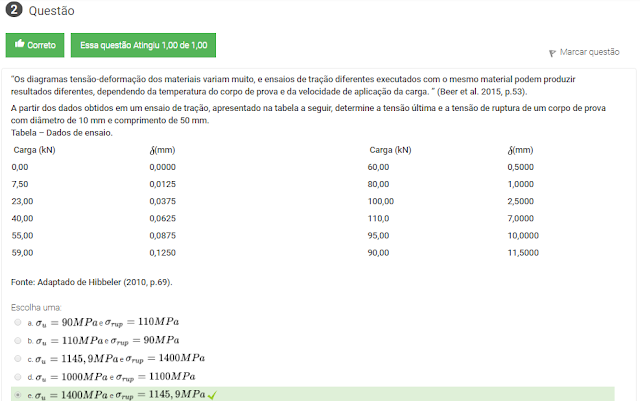
A partir dos dados obtidos em um ensaio de tração, apresentado na tabela a seguir, determine a tensão última e a tensão de ruptura de um corpo de prova com diâmetro de 10 mm e comprimento de 50 mm.
Tabela – Dados de ensaio.
|
Carga (kN) |
|
|
Carga (kN) |
|
|
0,00 |
0,0000 |
60,00 |
0,5000 |
|
|
7,50 |
0,0125 |
80,00 |
1,0000 |
|
|
23,00 |
0,0375 |
100,00 |
2,5000 |
|
|
40,00 |
0,0625 |
110,0 |
7,0000 |
|
|
55,00 |
0,0875 |
95,00 |
10,0000 |
|
|
59,00 |
0,1250 |
90,00 |
11,5000 |
Fonte: Adaptado de Hibbeler (2010, p.69).
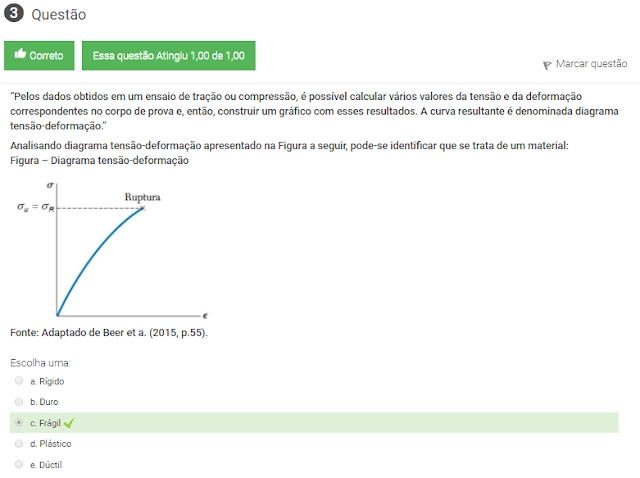
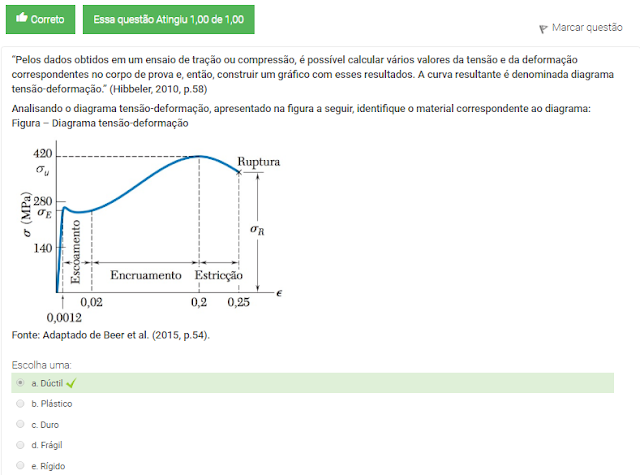
Analisando o diagrama tensão-deformação, apresentado na figura a seguir, identifique o material correspondente ao diagrama:
Figura – Diagrama tensão-deformação
Fonte: Adaptado de Beer et al. (2015, p.54).
A barra apresentada na figura a seguir é composta por dois segmentos AB e BD, com área de seção transversal Aab=500mm² e Abd=100mm², respectivamente. Determine o deslocamento vertical da extremidade A, sabendo-se que o módulo de elasticidade do material é de 200 GPa.
Figura – Desenho esquemático de uma barra
Fonte: Hibbeler (2010, p.89)
Um fio de nylon está submetido à força de tração de 10 N. Sabendo que E=3GPa e que o comprimento do fio é incrementado em 1,2%, determine o diâmetro do fio.