ELEMENTOS DE MÁQUINAS U1 - SEÇÃO 1 U1S1 - ATIVIDADE DIAGNÓSTICA
1) Para a questão da deflexão da mola helicoidal, aplicamos o teorema de Castigliano. Lembrando que a energia total de deformação de uma mola é composta de um componente torcional e outra de cisalhamento. Com isso podemos apresentar a equação [1.10] abaixo, que representa a deflexão de uma mola de compressão com fio redondo: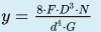
Em que y = deflexão da mola (em mm), N = número de espiras ativas, G = módulo de elasticidade por torção (em MPa).
A figura a seguir apresenta uma curva força-deflexão característica de uma mola helicoidal.
Figura – Curva força-deflexão.
Fonte: NORTON, Robert L.; Projeto de Máquinas: uma abordagem integrada. Porto Alegre: Bookman, p. 797, 2013
Podemos também expressar então a constante k da mola, apresentada na figura, sendo:
Concluindo temos a influência da curvatura quando a mola está sujeita a fadiga, e temos a deflexão da mola que nos leva a constante k da mola.
Observando a figura apresentada no texto-base, encontramos uma variável que chamamos de k, que representa a constante da mola. Qual a função desta constante? Escolha a alternativa correta abaixo.
Escolha uma:

2) Utilizando então uma mola helicoidal de compressão, podemos elaborar uma avaliação de esforços, e considerando que estamos em condição de equilíbrio estático, aplicamos uma força F de cisalhamento direta e um momento de torção T equação , onde:
T=F.D/2
Para D, diâmetro médio de espiral em mm. A tensão de cisalhamento máxima é a soma da tensão devido ao torque mais a tensão devido a força cisalhante no fio e pode ser obtida pela equação a seguir.
Tmax=(t.r/j)+(f/A)
Em que r é o raio (em mm) do fio de diâmetro d (em mm) da mola, J é o momento polar em mm4 e A é área em mm2.
Sabemos que para um fio circular, podemos alterar a equação da seguinte forma: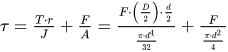
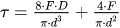
Quando utilizamos em uma mola helicoidal de compressão, um fio redondo, conseguimos definir a equação, demostrada no texto-base. Esta equação nos apresenta a tensão máxima de cisalhamento. Analise as alternativas abaixo e assinale a afirmativa correta.
3) Molas Helicoidais são elementos para uso industrial com uma vasta aplicação, sendo sua principal função a de armazenar energia de forma potencial e suportar tensões. Quando o sistema ou equipamento precisar, a mola atua. Também pode ser utilizada para amortecimento de vibrações.
Pensando que as molas precisam suportar tensões, escolha qual a alternativa a seguir apresenta as tensões que as molas suportam.
Escolha uma:
ELEMENTOS DE MÁQUINAS U1 - SEÇÃO 1 U1S1 - ATIVIDADE DE APRENDIZAGEM
1) A questão de estabilidade de uma mola helicoidal de compressão está relacionada com a possibilidade da mola flambar quando o comprimento for muito grande em relação a carga. Então, quando a deflexão for muito grande, teremos o problema de flambagem. Assim, devemos nos preocupar em prevenir este efeito. Para aplicações onde temos fio redondo e o material de construção for o aço podemos usar a equação a seguir:
Analisando o projeto uma mola helicoidal de compressão, encontramos o comprimento Lo com 150mm, e na comparação com a equação mencionada no texto-base, temos o seguinte resultado: 150 < 148. Com este resultado, qual das alternativas abaixo representa o resultado correto?
2) Quando damos forma a mola, ou seja, a enrolamos para formar a hélice e o diâmetro médio da espiral, temos um efeito de curvatura, que precisamos levar em consideração. Quando avaliamos somente em carregamento estático, normalmente desprezamos este efeito, mas já na condição de carregamento dinâmico, temos que avaliar melhor este efeito da curvatura, pois afeta na vida útil da mola, por fadiga.
Considerando que uma mola helicoidal, sendo aplicada para carregamento dinâmico, escolha uma das alternativas abaixo que representa uma afirmação correta.
Escolha uma:
3) Nos processos de produção de uma mola, devemos ter em conta que a curvatura da espiral é um fator importante, assim definimos um índice de mola C, e temos então:
Este índice, foi elaborado de forma experimental, pois se temos um índice muito pequeno, os equipamentos não conseguem manufaturar a mola sem provocar deformações indesejadas no perfil do fio, e do lado oposto, ou seja, quando o índice é muito grande a possibilidade de o fio não permanecer na área destinada ao processo de fabricação é elevada, e, assim, pode provocar defeitos ou mesmo a interrupção do processo produtivo. Isto foi comprovado através de vários anos de manufatura de molas.
O índice de mola C, é utilizado para se considerar os aspectos de fabricação de uma mola helicoidal. Assim, escolha uma única alternativa abaixo que esteja de acordo com o objetivo do cálculo do índice de mola.
ELEMENTOS DE MÁQUINAS U1 - SEÇÃO 2 U1S2 - ATIVIDADE DIAGNÓSTICA
1) Temos vários métodos de cálculo para isto, mas vamos usar um método chamado de critério de falha de Sines em fadiga torcional, pois as molas são livres de entalhes e as superfícies de contato são frequentemente bem lisas.
Este método é baseado em um estudo que demostra que temos os seguintes limites de resistência (Ssa = Limite de resistência à fadiga) em função do tipo de acabamento aplicado no processo de fabricação, sendo: sem jateamento de granalha, Ssa = 241 MPa, e com jateamento de granalha, Ssa = 398 MPa. Podemos observar que no ato de aplicarmos um jato de granalha (um tipo de esfera de metal) temos um aumento deste tipo de resistência mecânica. Nestes valores temos que aplicar o fator de segurança, que são determinados por algumas equações, sendo que Kb (fator Bergsträsser) o de maior utilização.
Ns=Ssa/Ta
Em um projeto de uma mola de compressão, que será aplicada em situações de alto nível de ciclos, tem-se que a mola teve um acabamento com um jateamento de granalha. Verificou-se que temos uma tensão ta=150MPa. Após vários ensaios práticos, foi comprovado que um fator de segurança de no mínimo de 1,5 seria suficiente para obtermos a vida infinita. Assim qual das alternativas abaixo pode ser aplicada para atender estas condições com menor custo?
Escolha uma:
2) Caso tenhamos a necessidade de projetar uma mola em alto volume de produção, existe um termo chamado fom, que é uma figura de mérito, que está associado a obtenção de um menor custo. Assim, uma fom pode ser estabelecida com a equação a seguir: 
Em que y = peso específico (Kg/mm³ ); d = diâmetro do arame (mm); Nt = número total de espiras e D = diâmetro das espiras (mm). Quando realizarmos a comparação entre aços, poderemos suprimir o peso específico.
No desenvolvimento do projeto de uma mola de compressão, encontramos algumas molas possíveis para uma mesma aplicação. Precisamos decidir então, o valor da fom (vide o texto-base) e, tenha em mente que o valor mais próximo de zero terá o menor custo para a fabricação desta mola. Encontre dentre as alternativas a seguir, a opção correta.
Escolha uma:
3) Temos várias situações industriais, em que os ciclos de operação são muito altos, como por exemplo, em compressores alternativos para ar comprimido. Tem-se que a fadiga é algo que queremos evitar a todo custo, para não termos quebras prematuras. Deste modo, buscamos o que chamamos de vida infinita para o projeto de molas helicoidais de compressão. Para isto, não podemos ultrapassar o valor de resistência do material (por exemplo: resistência a tração, resistência a compressão, etc.) , já aplicado um fator de segurança.
Temos um método que é baseado em um estudo que demostra que temos os seguintes limites de resistência (Ssa = Limite de resistência à fadiga) em função do tipo de acabamento aplicado no processo de fabricação, sendo: sem jateamento de granalha, Ssa = 241 MPa, e com jateamento de granalha, Ssa = 398 MPa. Podemos observar que no ato de aplicarmos um jato de granalha (um tipo de esfera de metal) temos um aumento deste tipo de resistência mecânica.
Observamos, a partir do texto-base, que no projeto de uma mola helicoidal de compressão, quando sujeita a uma enorme quantidade de ciclos, devemos avaliar o projeto desta mola, com a aplicação de um critério. Escolha dentre as alternativas qual é o critério correto.
Escolha uma:
ELEMENTOS DE MÁQUINAS U1 - SEÇÃO 2 U1S2 - ATIVIDADE DE APRENDIZAGEM
1) A frequência crítica de molas é um fator de análise importante em aplicações, requerendo um movimento alternativo rápido, como por exemplo, em molas para válvulas de motores de ciclo Otto. Nestas condições, a mola helicoidal pode sofrer quebra de forma antecipada e se romper a qualquer momento em função de ondas de ressonância. Para se prevenir isto, durante o projeto precisamos determinar a frequência fundamental da mola [f]. Para casos em que a frequência de trabalho é maior que f, devemos redimensionar a mola até que a frequência de trabalho seja menor que a frequência fundamental. Assim, temos a equação:
Em que k = razão de mola; g = aceleração da gravidade; W = peso da mola.
Para um projeto de uma mola de compressão, temos uma frequência de trabalho de 15 Hz. Para uma mola com K =3200 N/m ; W = 0,25N, e utilizando a constante da gravidade como sendo g=9,81m/s², qual das alternativas abaixo corresponde a que apresenta a frequência fundamental?
Escolha uma:
2) As molas podem ser manufaturadas por processos a quente ou a frio, lembrando que, para ser considerado processo a quente, o material deve estar acima da temperatura de recristalização do mesmo. A escolha do tipo de processo é uma função do tipo de material, do índice da mola (índice C) e das propriedades desejadas. Deste modo, precisamos saber qual será a aplicação da mola, para sabermos qual material e qual processo de fabricação utilizar.
Podemos visualizar alguns tipos de aços mais comumente utilizados, na tabela 01 a seguir.
Uma das características iniciais, quando trabalhamos com materiais para mola é a sua capacidade de resistência a tração [Sut], e neste momento precisamos escolher um diâmetro para o fio, sem o qual não conseguimos estipular a resistência a tração. Para o cálculo da capacidade de resistência a tração, temos a seguinte equação:
[1.18]
Em que A e m são constantes obtidas a partir da Tabela 02 e d é o diâmetro do fio.
Tabela 01 – Constantes A e m, para se estimar a resistência mínima de tração de fios comuns de mola.
Tabela 02 – Propriedades mecânicas de alguns fios de molas.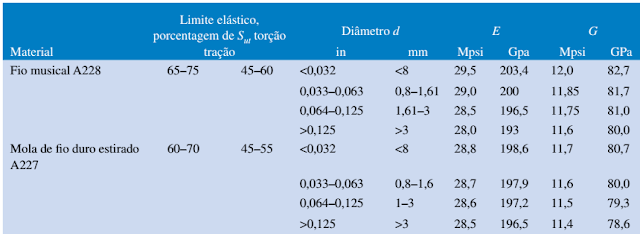
Utilizando a tabela 02, e o texto-base, precisamos escolher a alternativa abaixo que corresponda ao material que pode ser utilizado em um fio com diâmetro de 1,2mm e G = 80 GPa
Escolha uma:
3) Na análise da compressão estática de molas, devemos ter em consideração que no momento em que a mola está chegando ao seu final de curso, ou seja, está próxima ao fechamento das espiras, devemos determinar o que chamamos de força de fechamento [Fs]. Assim temos a equação a seguir: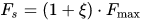
Em que E é o percurso fracionário até o fechamento (este percurso significa que nesta região até o fechamento a mola não deve trabalhar, sob risco de quebra do fio). Além das considerações que até o momento realizamos para o material de molas, devemos considerar em um projeto de molas, as seguintes condições:

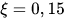
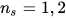
Em que C = índice da mola; Na = número de espiras ativas; ns = fator de segurança no fechamento (altura sólida).
Considerando um projeto de uma mola de compressão, em que temos uma Força máxima de 150 N, determine qual é a única alternativa em que atende aos fatores Fs= Força de fechamento ; C = índice de mola ; Na= número de espiras ativas; E= percurso fracionário até o fechamento ; e ns = fator de segurança, mencionados no texto base.
Escolha uma:

Figura – Mola de extensão – tipo de enrolamento.

As molas de extensão, com enrolamento fechado, apresentam uma maior precisão dimensional do que a mola de enrolamento aberto.
As molas de extensão são utilizadas para aplicações onde precisamos armazenar energia mecânica depois de aplicarmos tensões de tração. Quando temos uma mola de extensão com enrolamento fechado, escolha a alternativa correta.
Escolha uma:
a. A fabricação da mola com enrolamento fechado, permite uma menor tensão aplicada em relação ao de enrolamento aberto.
b. A fabricação da mola com enrolamento fechado permite uma maior precisão dimensional.
c. A fabricação da mola com enrolamento aberto tem característica de aumentar carga máxima
d. A fabricação da mola com enrolamento aberto permite uma maior precisão dimensional.
e. A fabricação da mola com enrolamento aberto é mais comum do que a de enrolamento fechado.

2) As molas Belleville (também conhecidas como mola prato) foram patenteadas na França por J. F. Belleville em 1897, tais molas apresentam, como característica, uma relação não linear entre força aplicada e a sua deflexão. Este tipo de mola é largamente aplicado quando temos uma carga elevada com uma pequena deflexão. Sob o ponto de vista dimensional, a mola Belleville, é bastante simples e podemos apresentar através da figura a seguir, um modelo mais usual deste tipo de mola.
Figura – Dimensões principais de uma mola Belleville.

Escolha uma:
a. A relação entre os diâmetros tem a função de não permitir a sua montagem.
b. A espessura da mola, não influencia na força da posição plana.
c. A razão entre os diâmetros influencia na força da posição plana.
d. A relação entre os diâmetros não influencia na força da posição plana.
e. A relação entre a altura h e a deflexão influencia na força da posição plana.

3) Para os casos em que as molas helicoidais estão sujeitas a torção em suas extremidades, podemos chama-las de molas helicoidais de torção. Usualmente elas são manufaturadas com enrolamento fechado, como uma mola de extensão, mas com um tensionamento inicial desprezível. Temos a equação da tensão de flexão máxima em [MPa] para uma mola helicoidal de torção, sendo: Em uma mola de torção, temos que obter a tensão de flexão máxima, para avaliar se ela atende a uma necessidade de projeto. Assim, com os seguintes dados: Força = 100 N, comprimento
Escolha uma:
a. 6777,32 MPa
b. 6637,77 Pa
c. 6627,64 MPa
d. 7235,66 MPa
e. 6524,32 Pa
ELEMENTOS DE MÁQUINASU1 - SEÇÃO 3U1S3 - ATIVIDADE DE APRENDIZAGEM
1) As molas Belleville foram patenteadas na França por J. F. Belleville em 1897, tais molas apresentam, como característica, uma relação não linear entre força aplicada e a sua deflexão. Este tipo de mola é largamente aplicado quando temos uma carga elevada com uma pequena deflexão. A figura a seguir nos mostra alguns tipos de formas de molas Belleville.
Figura – Molas Belleville.
Levando-se em conta o aspecto dimensional, a mola Belleville, é bastante simples e a figura a seguir ilustra um modelo mais comum deste tipo de mola.
Figura – Dimensões principais de uma mola Belleville.
Observando as características dimensionais de uma mola Belleville, podemos notar que o seu formato permite montar mais de uma mola sobre a outra, desde que sejam das mesmas dimensões. Quando realizamos esta montagem, qual a afirmação que está correta?
Escolha uma:
a. quando colocamos uma sobre a outra aumentamos a capacidade de carga, alterando a deflexão.
b. quando colocamos uma sobre a outra diminuímos a capacidade de carga, alterando a deflexão.
c. quando colocamos uma sobre a outra a capacidade de carga e a deflexão não se alteram.
d. quando colocamos uma sobre a outra aumentamos a capacidade de carga, sem alterar a deflexão.
e. quando colocamos uma sobre a outra diminuímos a capacidade de carga, sem alterar a deflexão.
2) A principal diferença das molas de extensão com relação as molas de compressão é que o seu uso é para armazenarmos energia mecânica. Nas molas de extensão quando aplicamos uma força em seus laços ou ganchos, e posteriormente, removemos esta força, a mola volta ao seu estado original de repouso.
Mola de extensão – Características construtivas principais.
Em uma mola de extensão, precisamos usar os ganchos ou laços para obtermos qual ação da mola? Assinale a alternativa que corresponda a resposta correta.
Escolha uma:
a. Ação de compressão da mola.
b. Ação de torção da mola.
c. Ação de flexão da mola.
d. Ação de torque da mola.
e. Ação de tração da mola.
3) Quando as molas helicoidais estão sujeitas a torção em suas extremidades, dizemos que elas são molas helicoidais de torção. Usualmente elas apresentam-se na forma de um enrolamento fechado, como uma mola de extensão, mas com um tensionamento inicial desprezível. Uma característica das molas helicoidais de torção, é a necessidade de se especificar a localização das extremidades, uma em relação a outra. A figura a seguir nos apresenta os ângulos característicos desse tipo de mola.
Figura – Ângulo de posicionamento da extremidade.

Observando a figura apresentada no texto-base, podemos identificar 3 ângulos que envolvem uma mola de torção. O que representa o ângulo
Escolha uma:
a. representa a posição final da extremidade da mola de torção sob carga.
b. representa a posição inicial da extremidade da mola de torção sem carga.
c. representa a posição inicial da extremidade da mola de torção sob carga.
d. representa a posição final da extremidade da mola de torção sem carga.
e. representa uma posição intermediária da extremidade da mola de torção, independente da carga.
ELEMENTOS DE MÁQUINASU1 - SEÇÃO 3U1 - AVALIAÇÃO DA UNIDADE
1) As molas Belleville, foram patenteadas na França por J. F. Belleville em 1897, as quais caracterizam-se por apresentar uma relação não linear entre força aplicada e ___________________. Este tipo de mola é largamente aplicado quando temos uma carga elevada com um pequeno deslocamento.
Marque a alternativa que contém o termo que preenche corretamente a frase:
Escolha uma:
a. a sua flexão
b. a sua deflexão
c. a sua frequência.
d. a sua vibração
e. o seu movimento
2) A frequência crítica de molas é um fator de análise importante em aplicações requerendo um movimento alternativo rápido, como por exemplo, em molas para válvulas de motores de ciclo Otto. Nestas condições, a mola helicoidal pode sofrer quebra de forma antecipada e se romper a qualquer momento, em função de ondas de ressonância. Para se prevenir isto, durante o projeto precisamos determinar a frequência fundamental da mola [f]. Para casos em que a frequência de trabalho é maior que f, devemos redimensionar a mola até que a frequência de trabalho seja menor que a frequência fundamental. Assim, temos a equação: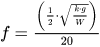
Em que k = razão de mola; g = aceleração da gravidade; W = peso da mola.
De acordo com a aplicação de uma mola helicoidal, em que temos uma frequência de trabalho de 8 Hz, um peso da mola de 0,25 N, uma aceleração da gravidade de 9,81 m/s² , e uma razão da mola de 4500N/m, verificar qual alternativa a seguir está correta.
Escolha uma:
a. frequência fundamental = 10,51 Hz, e deste modo a mola pode ser aplicada.
b. frequência fundamental = 7,52 Hz, e deste modo a mola não pode ser aplicada.
c. frequência fundamental = 10,51 Hz, e deste modo a mola não pode ser aplicada.
d. frequência fundamental = 6,57 Hz, e deste modo a mola pode ser aplicada.
e. frequência fundamental = 7,52 Hz, e deste modo a mola pode ser aplicada.
3) As molas podem ser manufaturadas por processos a quente ou a frio, lembrando que, para ser considerado processo a quente, o material deve estar acima da temperatura de recristalização do mesmo. A escolha do tipo de processo é uma função do tipo de material, do ________ da mola e das propriedades desejadas. Deste modo, precisamos saber qual será a aplicação da mola, para sabermos qual material e qual processo de fabricação utilizar. Uma das características iniciais, quando trabalhamos com materiais para mola é a sua capacidade de resistência a ________.
Marque a alternativa que contém os termos que preenche corretamente a frase, respectivamente, mencionado no texto-base.
Escolha uma:
a. da espira - compressão
b. da espira - tração
c. do índice - tração
d. da fase - tração
e. do índice - compressão
4) A partir da mola helicoidal de compressão vista na figura, é possível realizar uma análise de esforços com base na geometria desta mola. Considerando que a mola está em condição de equilíbrio estático, sob a ação de uma força axial F = 500 N, que provoca uma tensão de cisalhamento direta e um momento de torção T.
Utilizando ser D o diâmetro (mm) médio da espiral da mola e d o diâmetro do fio (mm), a tensão de cisalhamento máxima no fio pode ser obtida: 
Os valores do Diâmetro médio D e do diâmetro do fio d, respectivamente apresentados nos itens de (A) até (D), possuem as tensões máximas de cisalhamento no fio, apresentados nos itens de (I) até (IV).
A) 25mm e 1,2mm
B) 30mm e 1,4mm
C) 32mm e 1,5mm
D) 37mm e 2,7mm
I) 12355,14 N/mm²
II) 14245,06 N/mm²
III) 2480,76 N/mm²
IV) 18862,81 N/mm²
Marque a alternativa que contem a associação correta entre as dimensões do diâmetro D e do diâmetro d, com a respectiva tensão máxima de cisalhamento do fio, utilizando as informações contidas no texto base.
Escolha uma:
a. A – IV; B – II; C – I; D – III.
b. A – I; B – II; C – IV; D – III.
c. A – III; B – II; C – I; D – IV.
d. A – IV; B – III; C – I; D – II.
e. A – IV; B – I; C – II; D – III.
5) As tensões no corpo da mola de extensão são tratadas da mesma maneira que as molas de compressão, mas as molas de extensão têm em suas extremidades um gancho e estes sofrem deformação com tensões de flexão e torção. Podemos visualizar os pontos destas tensões na figura, onde a tensão em A é devida à força axial combinada e ao momento fletor, e a tensão no ponto B é decorrente da torção.
Figura – Características dos ganchos – Ponto A e B, e os raios r1 e r2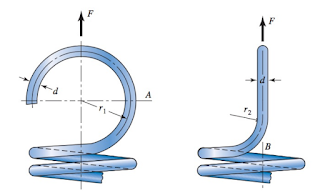
Fonte: BUDYNAS, Richard G.; NISBETT, J.Keith; Elementos de máquinas de Shigley. Porto Alegre: AMGH, p.527, 2016. Adaptado pelo autor.
A tensão máxima de tração no ponto A, devido a flexão, em [MPa], é dado por:
Definimos a tensão máxima torcional no ponto B, em [MPa], sendo: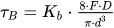
Podemos observar que nas molas de extensão, os ganchos são geralmente a parte frágil, com a flexão geralmente dominando como o ponto mais crítico desta região frágil.
Para uma mola de extensão com D = 26 mm; d = 2,0 mm; 12 mm; 6 mm;
Ka=1,068 e Kb=1,15, com uma força envolvida de 500 N, avaliar qual a alternativa a seguir que corresponde a tensão máxima que a mola pode suportar sem falhar.
Escolha uma:














