Dinâmica de Corpos Rígidos U4

DINÂMICA DE CORPOS RÍGIDOS U4 - SEÇÃO 1 U4 S1 - ATIVIDADE DIAGNÓSTICA

 

1) Leia atentamente a afirmativa a seguir.

Para descrever uma rotação intrínseca podemos usar um formalismo chamado ângulos de:

I - Euler.

II - Tait-Bryan.

III - Bose-Einstein.

Avalie quais das alternativas representam os nomes corretos de formalismos para a descrição de rotações intrínsecas.
Escolha uma:

2) I - Um referencial rotacionando no espaço, por ter mais liberdade para rotacionar, cria, além da força centrípeta, a força imaginária chamada centrosimétrica.

II - Um referencial no espaço que apresenta uma velocidade de translação constante e uma velocidade de rotação constante é um referencial inercial

III - Se um referencial em movimento de translação no espaço é acelerado em apenas um eixo, ele pode ser considerado um referencial inercial no plano perpendicular a aceleração (ou seja, nas outras duas coordenadas).

Leia com cuidado as três afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

3) I - O princípio de Galileu para dois referenciais inerciais pode ser aplicado no espaço tridimensional, basta utilizar vetores tridimensionais.

II - Uma rotação no espaço tridimensional é semelhante a uma rotação no plano, pode ser descrita por um único ângulo.

III - Para um movimento geral no espaço precisamos adicionar uma dimensão pra translação e rotação. Logo teremos três coordenadas para translação e duas para rotação.

Leia com cuidado as três afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

 DINÂMICA DE CORPOS RÍGIDOS U4 - SEÇÃO 1 U4 S1 - ATIVIDADE DE APRENDIZAGEM

 

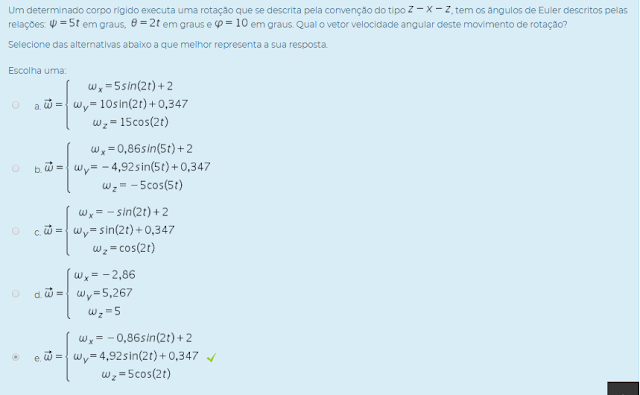
1) Um determinado corpo rígido executa uma rotação que se descrita pela convenção do tipo Z- X - Z tem os ângulos de Euler descritos pelas relações: Ψ = 5t em graus, Θ = 2t em graus e φ = 10 em graus. Qual o vetor velocidade angular deste movimento de rotação?
Selecione das alternativas abaixo a que melhor representa a sua resposta.

2) Para descrever uma rotação entorno de um ponto podemos utilizar um conjunto de até três rotações intrínsecas no plano. Tipicamente, estas rotações podem ser abordadas de duas convenções distintas, sendo que uma delas é conhecida como ângulos de Euler. Nos ângulos de Euler, o ultimo eixo de rotação deve ser o mesmo que o primeiro, como por exemplo na convenção x-z-x.

Selecione nas alternativas aquela que apresenta apenas rotações que seguem a convenção dos ângulos de Euler.
Escolha uma:

3) Um braço mecânico carrega uma ferramenta cujo um movimento de rotação corresponde uma rotação ao redor de um ponto. Pelo formalismo de Euler, sabemos que podemos representar esse movimento geral por um conjunto de rotações planas, e depois compor tais movimentos em uma matriz de rotação.

Marque a alternativa que indica o número máximo de rotações planas necessário para compor uma rotação qualquer ao redor de um ponto.
Escolha uma:

 DINÂMICA DE CORPOS RÍGIDOS U4 - SEÇÃO 2 U4 S2 - ATIVIDADE DIAGNÓSTICA

1) I - A distribuição de massa de um corpo rígido tridimensional determina uma grandeza chamada tensor de inércia, que é um extensão do momento de inércia para rotações sobre o plano, e que permite a análise de rotações tridimensionais.

II - O momento angular no espaço tridimensional deve ser descrito por três equações escalares independentes.

III - O momento linear no espaço tridimensional deve ser descrito por três equações escalares independentes.

Leia com cuidado as três afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

2) I - A energia cinética de rotação de um corpo rígido no espaço deve considerar a energia cinética de rotação entorno de cada eixo de rotação.

II - A energia cinética de translação de um corpo rígido sempre vai variar quando estiver sob a ação de uma força resultante não nula.

III - A energia cinética de um corpo rígido está relacionada com o quadrado da velocidade angular nos três eixos e também com o quadrado da velocidade linear do centro de massa. 

Leia com cuidado as três afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

3) I - O princípio de impulso e quantidade de movimento angular não se aplica ao espaço tridimensional pois não é possível descrever rotações no espaço tridimensional.

II - O princípio do trabalho e conservação de energia se aplica ao espaço tridimensional, uma vez que a translação e a rotação são analisadas de forma independente.

III - O princípio de impulso e quantidade de movimento linear se aplica ao espaço tridimensional somente se o corpo rígido não estiver executando um movimento de rotação. 

Leia com cuidado as três afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

 DINÂMICA DE CORPOS RÍGIDOS U4 - SEÇÃO 2 U4 S2 - ATIVIDADE DE APRENDIZAGEM

 

1) A placa fina uniforme tem uma massa de m=10Kg. No instante mostrado na figura ela está na iminência de enganchar seu canto A num gancho e se move a uma velocidade VG=10m/s= 10 m/s. Determine sua velocidade angular logo após o canto A acertar o gancho.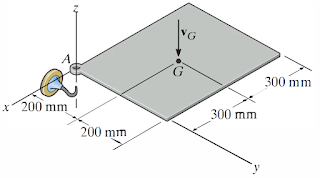

Selecione nas alternativas abaixo a que melhor representa sua resposta.
Escolha uma:

2) Cada um dos dois discos mostrados na figura tem uma massa de m=10KG e interligados por um eixo de massa muito menor que dos discos. Se a montagem gira em relação ao eixo Z a Wz=6rad/s fazendo com que os discos rolem sem deslizar, determine sua quantidade de movimento angular em relação ao eixo Z.


Selecione nas alternativas abaixo a que melhor representa sua resposta.
Escolha uma:

3) Leia atentamente as afirmativas abaixo.

I - A energia cinética de um corpo rígido no espaço tridimensional é composta pela energia cinética de translação e pela energia cinética de rotação, cada uma composta por pelo menos três componentes independentes.

II - A quantidade de movimento linear ou angular de um corpo rígido irá se conservar exceto na presença de uma força ou torque.

III - A velocidade angular de um movimento de rotação ao redor de um ponto pode ser descrita como um vetor tridimensional.

Leia com cuidado as três afirmativas anteriores, e assinale a alternativa que indica todas as afirmativas corretas.

Escolha uma:

 DINÂMICA DE CORPOS RÍGIDOS U4 - SEÇÃO 3 U4 S3 - ATIVIDADE DIAGNÓSTICA

 

1) Leia atentamente as afirmativas a seguir:

I - Para translação em três dimensões, as forças que agem sobre um corpo rígido no plano podem ser analisadas por meio de três equações escalares independentes.

II - Para descrever a posição do centro de massa de um corpo rígido em um problema tridimensional, precisamos de um vetor tridimensional, e nesse caso podemos fazer uso dos versores I, J e K.

III - Um corpo rígido no espaço tridimensional pode estar sujeito a ação de apenas três forças.

Assinale a alternativa correta, com relação às afirmativas indicadas.
Escolha uma:

2) I - Um corpo livre de torques é necessariamente um corpo livre, que não está sobre a ação de nenhuma força.

II - Um exemplo de corpos rígidos livres de torque é o de um satélite, pois ele está em um ambiente sem gravidade.

III - Um corpo livre de torques sempre conserva momento angular.

Leia com cuidado as três afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

3) I - Um giroscópio é um exemplo de corpo rígido que executa um movimento de rotação no espaço tridimensional.

II - Uma rotação no espaço tridimensional sempre pode ser construída com base em em três rotações planas.

III - Um corpo livre no espaço tridimensional pode estar sujeito a ação de apenas três torques. 

Leia com cuidado as três afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

 DINÂMICA DE CORPOS RÍGIDOS U4 - SEÇÃO 3 U4 S3 - ATIVIDADE DE APRENDIZAGEM

 

1) Um pião de 3KG está preso por uma junta esférica que não oferece atrito, como mostrado na figura. Sabendo que o raio de giro entorno do eixo de simetria do pião pode ser aproximado ao de um cone. Determine qual a velocidade de precessão WP que faz com que o pião precessa a um ângulo de ângulo=45º ao mesmo tempo que o momento de inércia entorno do eixo transversal é o dobro do momento de inércia do eixo de simetria e sua velocidade de rotação é de WS=5000rad/s. Considere que o centro de massa do pião também pode ser aproximado pelo de um cone.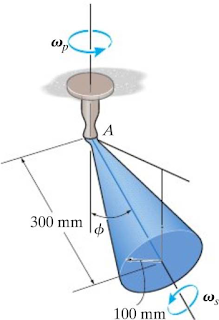


Selecione dentre as alternativas abaixo a que melhor represente a sua resposta
Escolha uma:

2) (Kroton) Dinâmica de Corpos Rígidos - A engrenagem mostrada na figura abaixo possui uma massa de 10kg e está montada em um ângulo de 10° com o eixo de rotação. Se Iz = 0,1 kg. m^2 , Ix = Iz = 0,5 kg. m^2 e o eixo está girando com uma velocidade angular constante ω = 30 rad/s. 



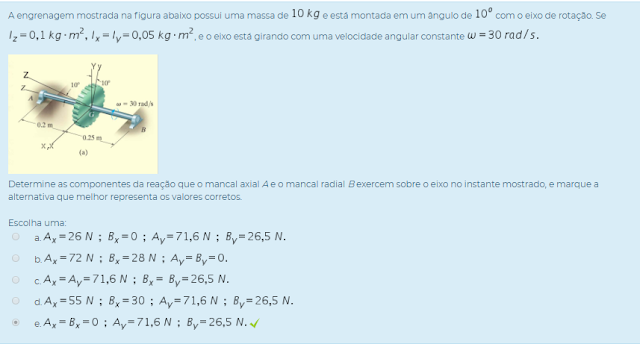
Determine as componentes da reação que o mancal axial A e o mancal radial B exercem sobre o eixo no instante mostrado, e marque a alternativa que melhor representa os valores corretos.

Escolha uma:

3) Dinâmica de Corpos Rígidos. Sabe-se que um satélite espacial de massa m é dinamicamente equivalente a dois discos finos de massas iguais. Os discos têm raio a = 800 mm estão rigidamente conectados por uma barra leve de comprimento 2a. Inicialmente, o satélite está girando livremente em torno de seu eixo de simetria a uma frequência de 60 rpm, quando um meteorito de massa mo = m/1000 viajando a uma velocidade vo = 2000 m/s em relação ao satélite, colide com ele e fica alojado no ponto C. 



F. Beer, Mecânica Vetorial para engenheiros: Dinâmica, 9ª edição, Porto Alegre, AMGH Editora Ltda, 2009.

Considere os momentos de inércia (figura em anexo).

Determine a magnitude da nova velocidade angular do satélite imediatamente após o impacto, e selecione a alternativa que melhor representa a resposta correta.

 DINÂMICA DE CORPOS RÍGIDOS U4 - SEÇÃO 3 U4 - AVALIAÇÃO DA UNIDADE

 

1) Calcule o efeito de uma rotação entorno do eixo x sobre um vetor que inicialmente estava na direção descrita pela relação r=10i+2K . Além do eixo de rotação mencionado considere que o ângulo da rotação é de ALPHA=90.

Selecione nas alternativas abaixo a que melhor representa a sua resposta.
Escolha uma:


2) Um disco homogêneo ilustrado na figura abaixo que possui uma massa m equals 2 space k g e gira à taxa constante numa velocidade angular omega subscript 2 equals 10 space r a d divided by s em relação ao braço A B C, que por sua vez gira à taxa constante numa velocidade angular omega subscript 1 equals 3 space r a d divided by s em relação ao eixo y. O disco possui um raio r equals 200 space m m. Despreze a massa do braço A B C. Dado: momento de inércia de um disco: I subscript z equals fraction numerator m r squared over denominator 2 end fraction ; I subscript x equals I subscript y equals fraction numerator m r squared over denominator 4 end fraction.


Calcule a energia cinética do sistema, e marque a alternativa que contém seu valor correto.

Escolha uma: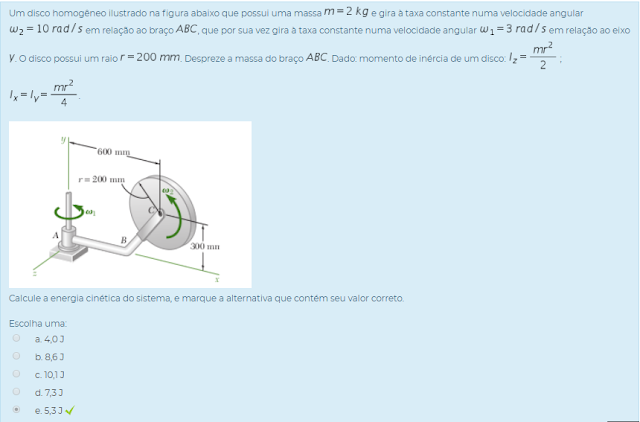


3) Na figura ilustrada abaixo que é composto por um sistema de disco e eixo, temos que o disco é homogêneo e possui uma massa m=3KG e gira à uma taxa constante W1=16 rad/s em relação ao braço ABC, que se encontra soldado ao eixo DCE que gira à taxa constante W2=8rad/s . O disco possui um raio r=200mm .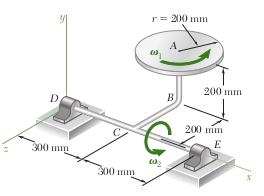

Determine a quantidade de movimento angular Ha do disco em relação a seu centro A e marque a alternativa que contém o valor correto.
Escolha uma: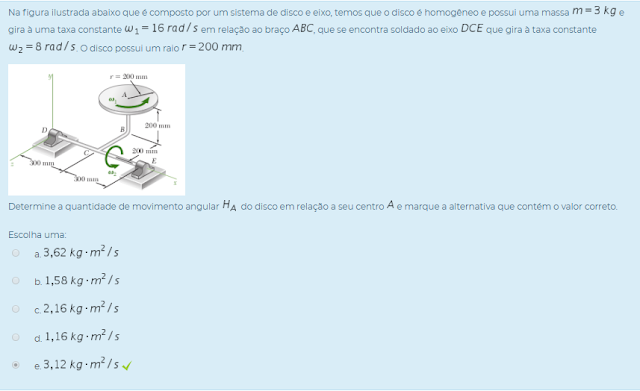



4) Um braço robótico segue a convenção X-Y-Z para rotações intrínsecas. Calcule a matriz de rotação seguindo esta convenção considerando que os ângulos de Tait-Bryan da primeira rotação tem um ângulo de 30º, o da segunda tem um ângulo de 45º e da última um ângulo de 60º.

Selecione dentre as alternativas abaixo, a resposta que indica a matriz de rotação correta para o caso indicado.
Escolha uma: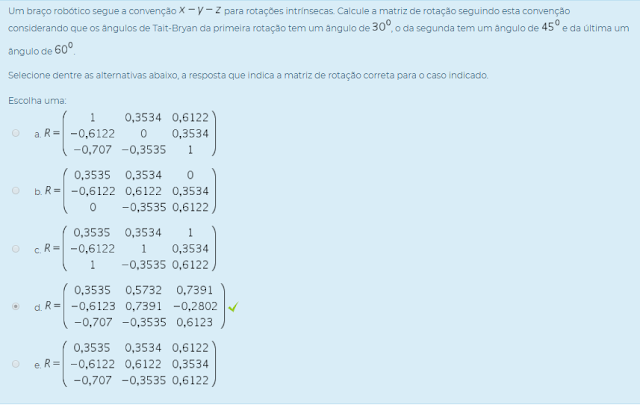


5) O primeiro satélite lançado pelo homem denominado Sputnik 1 era uma esfera metálica de raio R=58cm com quatro antenas externas, e que ao todo pesava 83,6KG. Logo depois de seu lançamento foi possível observar que seu momento angular era bastante alto. É importante notar que um satélite se comporta como um ______, e que sua rotação no espaço é bem descrita, na convenção dos ângulos de _____, por três ângulos, chamados _____, ______, _____.

Marque a alternativa que completa corretamente as lacunas do texto acima
Escolha uma: