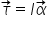Dinâmica de Corpos Rígidos U2

DINÂMICA DE CORPOS RÍGIDOS U2 - SEÇÃO 1 U2 S1 - ATIVIDADE DIAGNÓSTICA

1) Sejam as afirmativas a seguir:

I. O momento de inércia é também conhecido como inércia rotacional, ou massa angular.

II. O momento de inércia quantifica a resistência que um corpo tem em girar sobre um eixo, isto é, sofrer uma aceleração angular.

III. O momento de inércia total de um sistema é igual à soma individual de cada momento angular de seus constituintes.

Analise as três afirmativas do enunciado, e selecione a alternativa correta.
Escolha uma:

2) O momento de inércia tem unidade no Sistema Internacional de _________. Esta grandeza física nos permite descobrir a quantidade de torque que um corpo rígido precisa para a mudança de estado de movimento em torno de um eixo de rotação, por isso também é conhecido como__________. É uma propriedade _________(aditiva) do corpo, ou seja, a soma dos momentos de inércia de um sistema de corpos é igual à soma individual de cada um de seus constituintes.

Leia o texto e selecione a alternativa que melhor completa as lacunas.
Escolha uma:

3) Sejam as seguintes afirmativas:

I. O Centro de Massa é um ponto único no corpo rígido, onde se uma força for aplicada sobre uma linha que o atravessa não se gera torque.

II. Girar um disco é tão difícil quanto girar um anel de mesmo raio, basta que ambos possuam a mesma massa.

III. Para determinar a inércia de rotação de uma engrenagem, não basta saber apenas a sua massa.

Analise as três afirmativas anteriores, e selecione a alternativa correta.
Escolha uma:

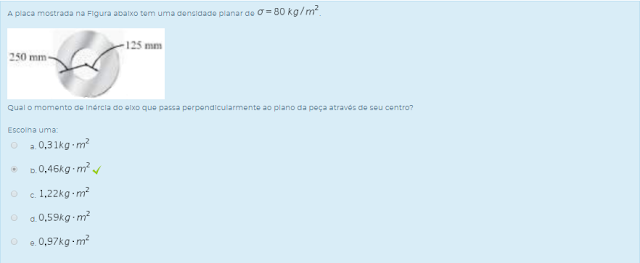
DINÂMICA DE CORPOS RÍGIDOS U2 - SEÇÃO 1 U2 S1 - ATIVIDADE DE APRENDIZAGEM

1) A placa mostrada na Figura abaixo tem uma densidade planar de

Qual o momento de inércia do eixo que passa perpendicularmente ao plano da peça através de seu centro?
Escolha uma:

2) Leia o texto a seguir com atenção:

Teorema dos ______________: Se conhecermos o momento de inércia em relação a um eixo que passa pelo Centro de Massa de um corpo rígido, o momento de inércia em relação a qualquer outro eixo paralelo ao original será: ______________.

Teorema dos ______________: Se conhecermos o momento de inércia de dois eixos, e estes definem um plano , o momento de inércia de um terceiro eixo , perpendicular a esse plano, será: ______________.

Leia o texto anterior com bastante atenção, e selecione a alternativa que melhor completa as lacunas do texto.
Escolha uma

3) Uma barra feita de material homogênea possui uma densidade linear definida pela relação

, onde é a distância à uma das extremidades da barra, como mostrado na figura abaixo, e as unidades estão no SI. Sabendo que a barra em questão tem um comprimento total de 2 metros.

Figura: Densidade da barra

Selecione, dentre as alternativas aquela que corresponde a massa total da barra.
Escolha uma:

DINÂMICA DE CORPOS RÍGIDOS U2 - SEÇÃO 2 U2 S2 - ATIVIDADE DIAGNÓSTICA

1) Um referencial não inercial terá sempre forças denominadas imaginárias que são uma consequência da Primeira Lei de Newton, ou Lei da Inércia. Referenciais linearmente acelerados e referenciais girantes são exemplos onde tais forças imaginárias estarão presentes.

Considere as alternativas a seguir e selecione a que contém apenas forças imaginárias ou inerciais.
Escolha uma:

2) Para o sistema mostrado na figura seguinte, uma uma viga de 2 KG está suspensa por duas barras cuja massa é muito inferior à massa da viga. No exato instante ilustrado na imagem as barras de sustentação balançam com uma velocidade angular W= 5 rad/s no sentido anti-horário.

Figura: Viga suspensa

Determine a tração T desenvolvida nas barras nesse instante e selecione a alternativa que apresente a resposta correta.
Escolha uma:

3) Leia as três afirmativas a seguir:

I. A soma de todas as forças que agem sobre um corpo rígido é igual à massa do corpo vezes a aceleração de seu centro de massa

II. Um referêncial girante e um referêncial acelerado são exemplos de um referêncial não inercial

III. A primeira lei de Newton, também chamada Lei da Inércia, diz que não é possível alterar o estado de movimento de um corpo.

Leia com cuidado as três afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

DINÂMICA DE CORPOS RÍGIDOS U2 - SEÇÃO 2 U2 S2 - ATIVIDADE DE APRENDIZAGEM

1) Leia as três afirmativas a seguir:

I - A soma de todas as forças que agem sobre um corpo rígido é igual à massa do corpo vezes a aceleração de seu centro de massa

II - Um referencial girante e um referencial transladando a velocidade constante são exemplos de referencial inercial

III - Forças imaginárias são uma consequência direta da primeira lei da Termodinâmica, a chamada Lei da Entropia.

Leia com cuidado as três afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

2) No instante mostrado na figura abaixo os dois membros AB e CD giram com uma velocidade angular w=6 rad/s. Entretanto, o sistema gira livremente, e está sob a influência da gravidade no instante estudado. A massa total da viga sustentada pelos membros é de 50Kg e seu centro de massa é mostrado em G. Os dois membros de sustentação tem massa desprezível quando comparada a viga. Considere a gravidade como 10 m/ s²

Determine a aceleração centrípeta e tangência do centro de massa do centro de massa do sistema e selecione a opção que melhor represente sua resposta.
Escolha uma:

3) Na figura temos a representação de um mecanismo de pistão conhecido como Jugo Escocês. O sistema tem uma massa total de 50Kg cujo centro de massa está representado pelo ponto CM. Além disso a equação de movimento do centro de massa é xd(t)=15+5cos(10t) em unidades do SI.

Qual a força resultante que atua sobre o centro de massa no referencial do próprio centro de massa? Despreze os efeitos da gravidade, considere o movimento do centro de massa sobre o eixo x e selecione a opção que melhor represente sua resposta, na unidade Newton.
Escolha uma:

DINÂMICA DE CORPOS RÍGIDOS U2 - SEÇÃO 3 U2 S3 - ATIVIDADE DIAGNÓSTICA

1) I. Um referencial executando um movimento de rotação está sujeito a forças inerciais.

II. Torque é definido como o produto vetorial entre a força F e o raio r , ou seja T=F X r .
III. Se o deslocamento for dado por: x(t) ; a velocidade será dada por v=dx/dt, e a aceleração por
Leia as afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

2) Leia as três afirmativas a seguir:

I. A força de coriolis é outro exemplo de força imaginária ou inercial.
II. A unidade de torque no Sistema Internacional (SI) é: N.m /Kg.

III. Se para definir uma posição angular usarmos graus, podemos definir a velocidade angular em: graus / s².

Leia com atenção as afirmativas e assinale qual alternativa é a correta.
Escolha uma:

3) Numa rotação recomenda-se usar coordenadas ______ para descrever o movimento. Durante a rotação o _____ permanece constante e apenas o ________ deve mudar, por isso, a cinemática do nosso sistema será descrito pelas grandezas denominadas ____________, ____________.

Leia o texto acima e selecione a alternativa que melhor completa as lacunas.
Escolha uma:

DINÂMICA DE CORPOS RÍGIDOS U2 - SEÇÃO 3 U2 S3 - ATIVIDADE DE APRENDIZAGEM

1) O navio mostrado na figura abaixo tem uma massa de e seu centro de gravidade está localizado em G. Dois rebocadores de peso desprezível são usados para virá-lo, cada um com uma força de 10 KN. Considere que o navio tem um raio de giro em relação ao seu centro de gravidade de 37.5 M . Um rebocador esta distante em 30m do centro de massa do navio, o segundo está a 60m do centro de massa. Despreze a resistência da água.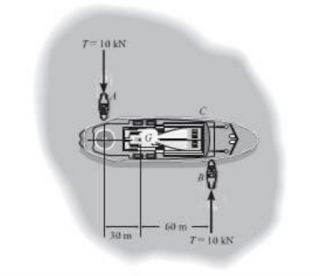

Determine a intensidade inicial da aceleração angular desprezando a resistência da água. Selecione a alternativa que represente melhor a solução encontrada.
Escolha uma:

2) Leia as três afirmativas a seguir:

I. A soma de todas as forças que agem sobre um corpo rígido é igual à massa do corpo vezes a velocidade de seu centro de massa.

II. Um referencial girante a uma velocidade angular constante e um referencial transladando a velocidade linear constante são ambos exemplos de referencial inercial.

III. A aceleração centrípeta de um sistema é proporcional ao quadrado da velocidade tangencial deste mesmo sistema, seguindo a relação ac = v²/r.

Leia com atenção as afirmativas anteriores, e assinale qual alternativa é a correta.
Escolha uma:

3) Na figura abaixo está uma roda montada em um eixo fixo possui uma massa de 50kg e um raio de giro em relação ao eixo Z de 150mm . A correia mostrada possui massa desprezível e está submetida a uma força 150N. Considere que o escorregamento entre a superfície da correia e a roda é nulo.

Figura: Sistema roda e correia

Determine a intensidade da aceleração angular da roda e selecione a alternativa que represente a solução encontrada.
Escolha uma:

DINÂMICA DE CORPOS RÍGIDOS U2 - SEÇÃO 3 U2 - AVALIAÇÃO DA UNIDADE

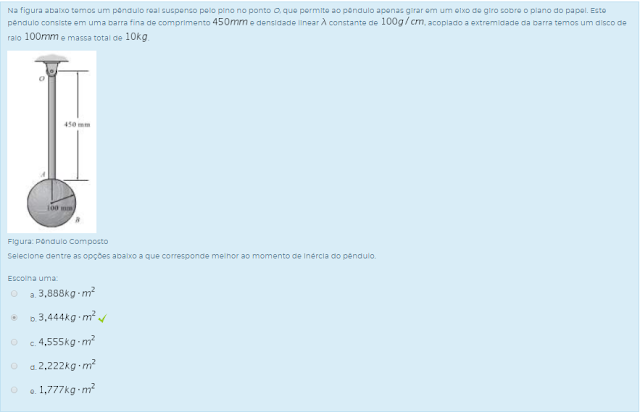
1) Na figura abaixo temos um pêndulo real suspenso pelo pino no ponto O, que permite ao pêndulo apenas girar em um eixo de giro sobre o plano do papel. Este pêndulo consiste em uma barra fina de comprimento 450 mm e densidade linear constante de 100g/cm, acoplado a extremidade da barra temos um disco de raio 100mm e massa total de 10Kg.

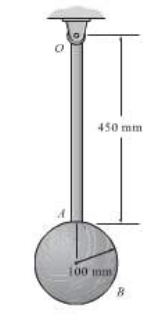
Figura: Pêndulo Composto

Selecione dentre as opções abaixo a que corresponde melhor ao momento de inércia do pêndulo.
Escolha uma:

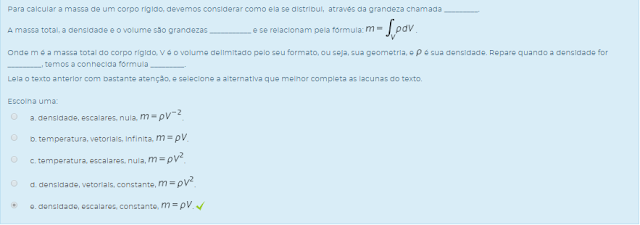
2) Para calcular a massa de um corpo rígido, devemos considerar como ela se distribui, através da grandeza chamada _________.

A massa total, a densidade e o volume são grandezas ___________ e se relacionam pela fórmula:

.
Onde m é a massa total do corpo rígido, V é o volume delimitado pelo seu formato, ou seja, sua geometria, e

é sua densidade. Repare quando a densidade for _________, temos a conhecida fórmula _________.

Leia o texto anterior com bastante atenção, e selecione a alternativa que melhor completa as lacunas do texto.
Escolha uma:

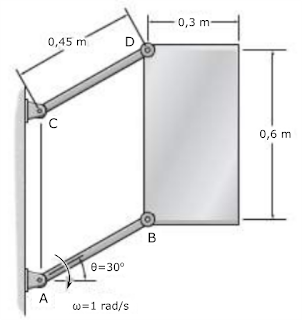
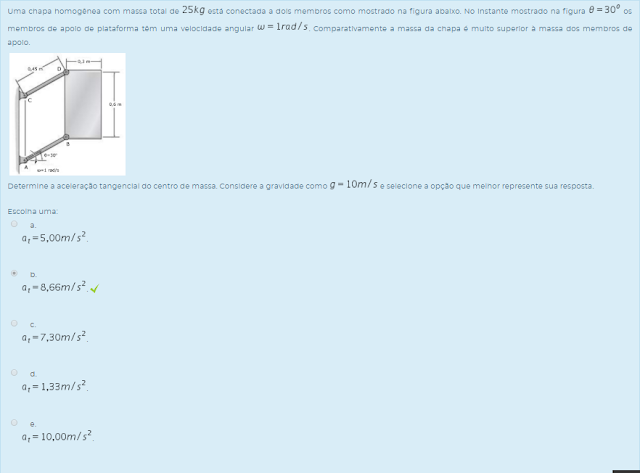
3) Uma chapa homogênea com massa total de 25Kg está conectada a dois membros como mostrado na figura abaixo. No instante mostrado na figura angulo= 30º os membros de apoio de plataforma têm uma velocidade angular w=1rad/s. Comparativamente a massa da chapa é muito superior à massa dos membros de apoio.

Determine a aceleração tangencial do centro de massa. Considere a gravidade como g=10m/s e selecione a opção que melhor represente sua resposta.
Escolha uma:

4) Um recipiente uniforme de 4 toneladas é suspenso pelo guindaste mostrado na figura abaixo. No exato momento da figura todo o sistema está sendo içado com uma aceleração de 1m/s², considere também que a massa da viga de suspensão BD é de 100Kg.

Qual a força dos membros AB, CD, EF, GH? Selecione a opção que melhor represente sua resposta.
Escolha uma:

5) Se o deslocamento angular for dado por: O(t); a aceleração angular é dada pela segunda ________________ de o(t) :

Torque pode ser escrito na mesma forma que a segunda lei de Newton, onde o ______________ faz as vezes da massa para a __________________

O movimento de um corpo rígido no plano é descrito por três equações escalares independentes, duas referente ao movimento ___________: EFx=max; EFY=may; e uma referente ao movimento _____________:

.

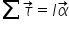
Leia o texto acima e selecione a alternativa que melhor completa as lacunas
Escolha uma: