Dinâmica de Corpos Rígidos U1

Dinâmica de Corpos Rígidos /U1 - Seção 1 /U1S1 - Atividade Diagnóstica

1) Em física podemos representar as grandezas como escalar e vetorial. As grandezas escalares precisam apenas de seu valor para ser determinadas, como por exemplo, a massa de corpos rígidos. Já grandezas vetoriais precisam de três características para serem descritas de maneira completa.

Marque a alternativa correta que contenha as três características necessárias para determinar e descrever completamente uma grandeza vetorial.
Escolha uma:


a. intensidade, direção, sentido 
b. aceleração, velocidade, posição 
c. momento, velocidade, direção 
d. potência, energia, trabalho 
e. momento, energia, trabalho 

2) Um engenheiro está analisando, em um de seus trabalhos, o centro de massa de um corpo rígido que possui sua posição descrita pelo seguinte vetor no plano Euclidiano, R=(3;4), em um sistema de referências onde o sistema de unidades utilizados para distâncias é em quilômetros (km).

Calcule o módulo do vetor e marque a alternativa correta.
Escolha uma:

a. 5 km 
b. 9 km 
c. 10 km 
d. 16 km 
e. 25 km 

3) Analise as afirmativas a seguir:

I) De posse do vetor posição de um ponto do corpo rígido como função do tempo, podemos obter a velocidade desse ponto através da derivada da posição em relação ao tempo.

II) Corpos rígidos são extensos, dotados de infinitos pontos. É importante que um engenheiro seja capaz de selecionar alguns pontos de interesse e descrever seu movimento em termos de posição, velocidade e aceleração, para ser capaz de projetar mecanismos eficientes.

III) Um ponto em um corpo rígido que gira com velocidade angular constante ao redor de um eixo de rotação, a uma distância R deste, possui o módulo da velocidade tangencial dada pela relação V=W.R.


Marque a seguir a alternativa que contém apenas as afirmativas verdadeiras:
Escolha uma:

a. I. 
b. III. 
c. I, II e III. 
d. I e II. 
e. I e III.

 Dinâmica de Corpos Rígidos /U1 - Seção 1 /U1S1 - Atividade de Aprendizagem

 

1) Um engenheiro precisa analisar um braço mecânico, a pedido de seu chefe, para elaborar um relatório de segurança. Em determinado instante, o manipulador do braço mecânico possui as seguintes coordenadas cartesianas no espaço (x,y,z)=(3,4,1), ou seja, o seu vetor posição. Para completar seu relatório, ele precisa indicar as posições do objeto em coordenadas cilíndricas, considerando que ambos os sistemas de coordenadas possuem a mesma origem e o mesmo eixo z.


Calcule a posição do ponto em coordenadas cilíndricas, e selecione a alternativa que o indica corretamente.
Escolha uma:


a.(5,arctan(4/3),5)  
b. (5,arctan(4/3),1)  
c. (1,arctan(3/4),5)  
d.(5,arctan(3/4),1)  
e.(1,arctan(4/3),5)  

2) Um engenheiro precisa realizar análises sobre o movimento de um ponto B na extremidade de um corpo rígido, que possui sua posição com relação ao eixo de rotação descrita pelo vetor R=(1;-1;0)   e sua velocidade angular descrita pelo vetor W(1;0;1). As unidades de grandeza do problema se encontram no Sistema Internacional (SI). 

Selecione a alternativa que contém o vetor velocidade (tangencial) do ponto B na extremidade do corpo rígido.
Escolha uma:

a. (1;1;-1) 
b.(-2;-1;3)  
c.(3;-3;0)  
d.(4;3;1)  
e.(-3;4;5)  

3) Um engenheiro está fazendo um relatório sobre um dispositivo mecânico, na empresa em que trabalha, onde precisa calcular posição de um sensor. Em um determinado instante, o corpo rígido analisado possui as seguintes coordenadas cartesianas no plano cartesiano (X,Y)=(3;4), ou seja, o vetor posição. 

Calcule a posição do sensor em coordenadas polares, considerando que as origens de ambos os sistemas de coordenadas coincidem. Selecione a alternativa que indica corretamente a posição calculada.
Escolha uma:

a.(3,arctan(4/3))  
b.(4,arctan(4/3))  
c. (5,arctan(3/4))  
d. (4,arctan(3/4))  
e.(5,arctan(4/3)) 

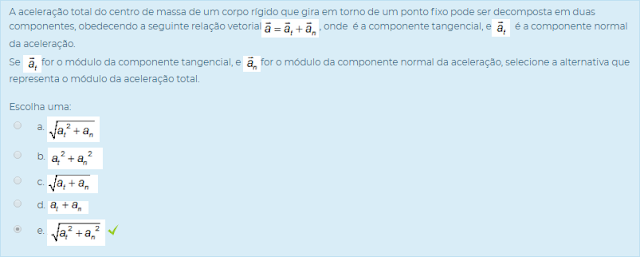
DINÂMICA DE CORPOS RÍGIDOS U1 - SEÇÃO 2 U1 S2 - ATIVIDADE DIAGNÓSTICA
1) A aceleração total do centro de massa de um corpo rígido que gira em torno de um ponto fixo pode ser decomposta em duas componentes, obedecendo a seguinte relação vetorial a=at+an, onde é a componente tangencial, e at é a componente normal da aceleração.

Se at for o módulo da componente tangencial, e an for o módulo da componente normal da aceleração, selecione a alternativa que representa o módulo da aceleração total.
Escolha uma:

2) Um engenheiro precisa fazer análises em um sistema mecânico, em uma indústria de automação. Verificando uma das partes móveis de um dispositivo, percebe que sua velocidade tangencial é dada pela seguinte função vetorial V(t)=3t² i . A unidade de grandeza da velocidade se encontra no SI.

Calcule o módulo da velocidade da parte móvel do dispositivo, no instante t=1s. Assinale a alternativa correta.
Escolha uma:

3) Um ponto na borda de um determinado corpo rígido, em formato de disco, descreve um movimento circular, preso em um ponto fixo que coincide com seu centro, e sua aceleração angular alpha(t) é dada pela seguinte função do tempo:

alpha(t)=30.t²

A unidade da aceleração está no SI.

Calcule o valor da aceleração angular para o instante t=2s. Assinale a alternativa correta.
Escolha uma:

 DINÂMICA DE CORPOS RÍGIDOS U1 - SEÇÃO 2 U1 S2 - ATIVIDADE DE APRENDIZAGEM

1) Um engenheiro precisa fazer análises em um sistema mecânico, em uma indústria de automação, onde trabalha. Verificando uma das partes móveis de um dispositivo, o engenheiro calcula que a velocidade de um ponto do corpo rígido é dada pela seguinte função vetorial: 

V(t)=eti, em unidades do SI.

A partir da velocidade, determine o módulo da aceleração de um ponto do corpo rígido, para o instante 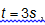 em unidades do SI. 
Escolha uma:

2) Um engenheiro precisa fazer análises em um sistema mecânico, em uma indústria de automação. Verificando uma das partes móveis de um dispositivo, recebe em um relatório que a posição de um ponto de interesse no interior do corpo rígido em função do tempo é dada por 

R(t)=3.sen(t)i+4.cos(t)i.

A partir de considerações geométricas, e da função posição dada no relatório, selecione a alternativa que descreve qual a trajetória do ponto no corpo rígido.
Escolha uma:

3) Um engenheiro foi contratado com o objetivo de fazer análises em um sistema mecânico, em uma indústria de automação. Verificando uma das partes móveis de um dispositivo, recebe em um relatório que a posição de um componente em função do tempo é dada por
R(t)=sen(t)i+cos(t)j   

A partir de considerações geométricas, e da função posição dada no relatório, selecione a alternativa que descreve qual a trajetória do corpo rígido.
Escolha uma:

 DINÂMICA DE CORPOS RÍGIDOS U1 - SEÇÃO 3 U1 S3 - ATIVIDADE DIAGNÓSTICA

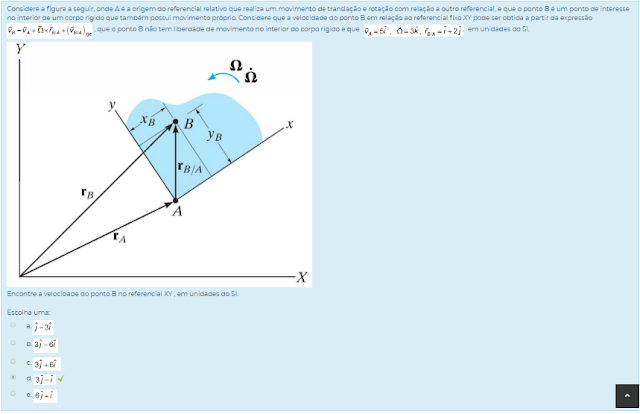
1) Considere a figura a seguir, onde A é a origem do referencial relativo que realiza um movimento de translação e rotação com relação a outro referencial, e que o ponto B é um ponto de interesse no interior de um corpo rígido que também possui movimento próprio. Considere que a velocidade do ponto B em relação ao referencial fixo XY pode ser obtida a partir da expressão 

, que o ponto B não tem liberdade de movimento no interior do corpo rígido e que ,, em unidades do SI.



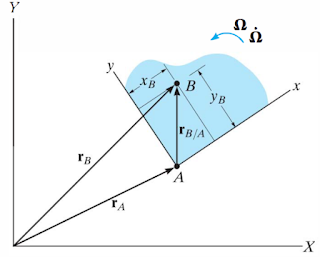
Encontre a velocidade do ponto B no referencial XY , em unidades do SI.
Escolha uma:

2) Leia atentamente as afirmativas a seguir:

I- O movimento planar de um corpo rígido é impossível de se descrever, pois um corpo rígido é composto por infinitos pontos e portanto esse movimento é muito complexo.
II- Um movimento geral de um corpo rígido no plano pode ser dividido em duas componentes principais: um movimento de translação e um movimento de rotação.
III- A análise do movimento planar pode ser simplificada por meio da definição de um referencial relativo que realiza uma translação, e ao redor do qual o corpo rígido gira.

Selecione a alternativa que marca todas as afirmativas corretas entre as sentenças acima
Escolha uma:

3) Considere a figura a seguir, onde A é a origem do referencial relativo que realiza um movimento de translação e rotação com relação a outro referencial, e que o ponto B é um ponto de interesse no interior de um corpo rígido que também possui movimento próprio.




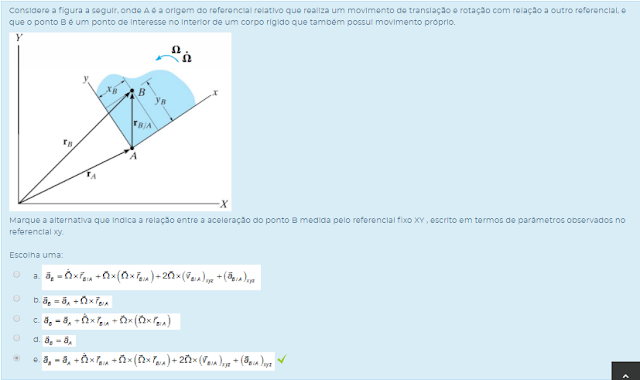
Marque a alternativa que indica a relação entre a aceleração do ponto B medida pelo referencial fixo XY , escrito em termos de parâmetros observados no referencial xy.
Escolha uma:

 DINÂMICA DE CORPOS RÍGIDOS U1 - SEÇÃO 3 U1 S3 - ATIVIDADE DE APRENDIZAGEM

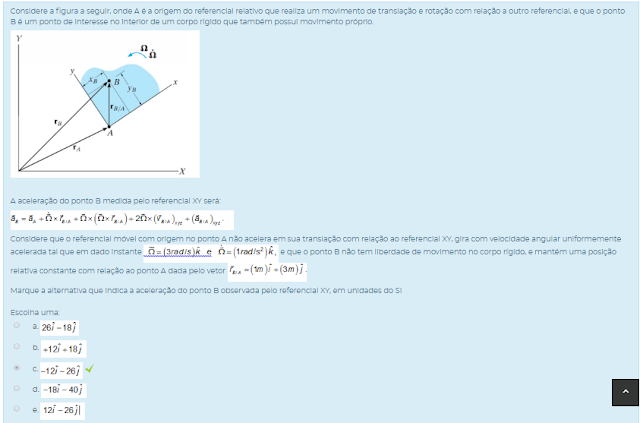
1) Considere a figura a seguir, onde A é a origem do referencial relativo que realiza um movimento de translação e rotação com relação a outro referencial, e que o ponto B é um ponto de interesse no interior de um corpo rígido que também possui movimento próprio. 

2) Leia atentamente a afirmação a seguir, que possui algumas lacunas

O __________, ou centro instantâneo de rotação é definido como um ponto fixo (ou referencial) em um corpo rígido, em movimento planar, que possui velocidade _______ em um determinado instante de tempo.

Leia o texto anterior, e assinale a alternativa que completa as lacunas do texto corretamente.
Escolha uma:

3) Na figura, vemos a ilustração de uma roda de um carro, que se move para a direita com velocidade constante. A roda possui raio de comprimento R, e o ponto A é seu centro. Na ilustração temos cinco pontos distintos, A, B, C, D, E. No instante que aparece na imagem, o ponto D faz um ângulo com a vertical. Suponha que a roda não desliza.




Analise as afirmativas indicadas a seguir:

I) Para um observador externo, em repouso sobre a calçada, o único ponto da roda que não se move no instante em questão é o ponto C.

II) O centro da roda, ponto A, tem 75% da velocidade do carro conforme relatado por um observador externo em repouso na calçada.

III) Se definirmos um referencial fixo na posição do ponto C, no instante em questão a velocidade observada para o ponto D é nula.

Marque a alternativa que indica todas as afirmativas corretas
Escolha uma:

 DINÂMICA DE CORPOS RÍGIDOS U1 - SEÇÃO 3 U1 - AVALIAÇÃO DA UNIDADE

1) Um determinado corpo rígido em formato de disco, descreve movimento circular, preso em um ponto fixo, e um ponto afastado de seu centro, próximo a borda possui sua aceleração angular alpha(t) dada pela seguinte função do tempo:

alpha(t) = 10.cos(t)

Calcule a velocidade angular do corpo rígido, considerando que inicialmente ela era 1rad/s, e selecione a alternativa correta.
Escolha uma:

2) Um engenheiro precisa realizar análises sobre o movimento de um ponto A no interior de um determinado corpo rígido, cuja velocidade angular é descrita pelo vetor omega=(1;1;1). A posição do ponto A com relação ao eixo de rotação é descrita pelo vetor R=(5;1;3). As unidades de grandeza se encontram no Sistema Internacional (SI).

Selecione a alternativa que contém o vetor aceleração normal do ponto A no interior do corpo rígido.
Escolha uma:

3) Um corpo rígido é colocado para girar ao redor de um eixo com velocidade algular descrita pelo vetor omega=(1;2;2). Um engenheiro precisa realizar análises sobre o movimento de um sensor que está localizado na superfície do corpo rígido, e possui sua posição com relação ao eixo de rotação descrita pelo vetor R=(2;1;0). As unidades de grandeza se encontram no Sistema Internacional (SI).

Selecione a alternativa que contém o vetor velocidade (tangencial) do corpo rígido.
Escolha uma:

4) Um engenheiro precisa fazer análises em um sistema mecânico, em uma indústria de automação. Verificando uma das partes móveis de um dispositivo, percebe que a velocidade de um determinado ponto do corpo rígido é dada pela seguinte função vetorial V(t) = 3t²i + 2tj.

Determine a função posição do ponto de interesse considerando que a partícula parte da origem, e selecione a alternativa correta.
Escolha uma:

5) Na figura podemos ver ilustração de um mecanismo composto de três barras. A barra OA de comprimento rA, a barra AB de comprimento rA/B, e a barra BC de comprimento rB, que estão fixadas mantendo a liberdade de rotação nos pontos O, A, B e C. No instante mostrado na figura, a barra BC gira no sentido anti-horário, em torno do ponto C, obrigando a manivela OA a girar em torno do ponto O. Supondo que no instante mostrado na figura, a barra BC girar com velocidade angular omegac=(5rad/S)k, e que seu comprimento seja rB=0,05m.



Marque a alternativa que contém o vetor velocidade correto, em unidades do SI, e que indica qual o sentido de rotação da barra OA em torno de O.
Escolha uma: