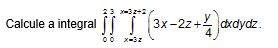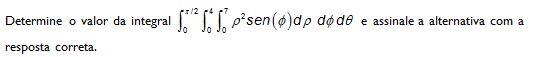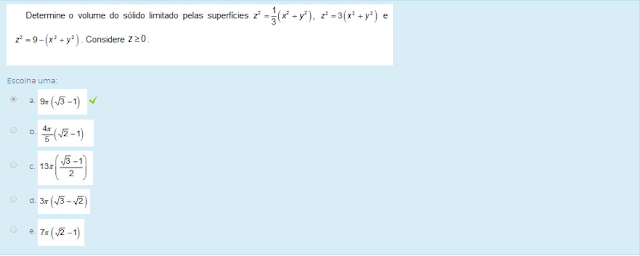Cálculo Diferencial e Integral III

CÁLCULO DIFERENCIAL E INTEGRAL III U2 - SEÇÃO 1 U2 S1 - ATIVIDADE DIAGNÓSTICA

 

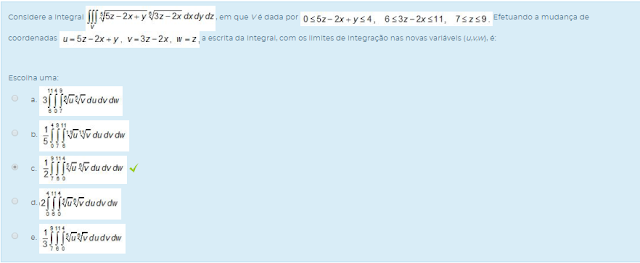
1) Considere a integral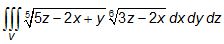 
, em que V é dada por 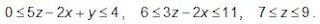Efetuando a mudança de coordenadas a escrita da integral, com os limites de integração nas novas variáveis (u,v,w), é:

Escolha uma:

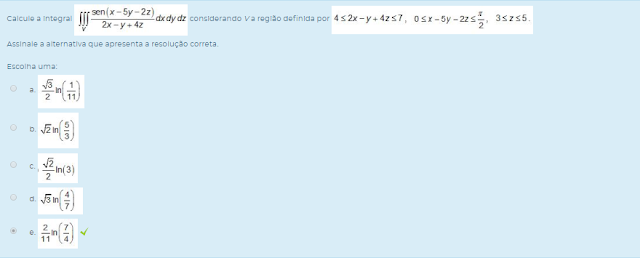
2) Calcule a integral considerando V a região definida por Assinale a alternativa que apresenta a resolução correta.
Escolha uma:

3) Considere a mudança de coordenadas:



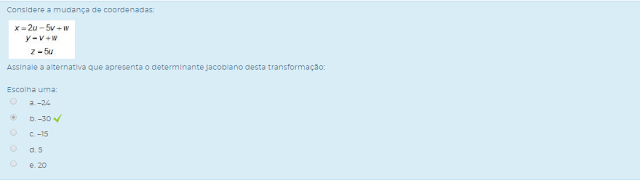
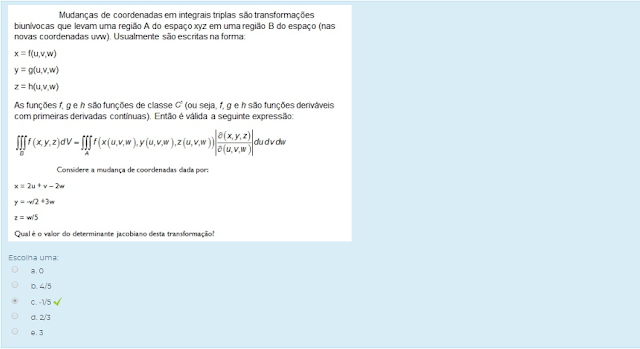
Assinale a alternativa que apresenta o determinante jacobiano desta transformação:
Escolha uma:

 CÁLCULO DIFERENCIAL E INTEGRAL III U2 - SEÇÃO 1 U2 S1 - ATIVIDADE DE APRENDIZAGEM

1) Considere o paralelepípedo definido por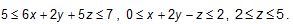 
O volume deste paralelepípedo é:
Escolha uma:

2) 
Escolha uma:

3) 
Escolha uma:

 CÁLCULO DIFERENCIAL E INTEGRAL III U2 - SEÇÃO 2 U2 S2 - ATIVIDADE DIAGNÓSTICA

 

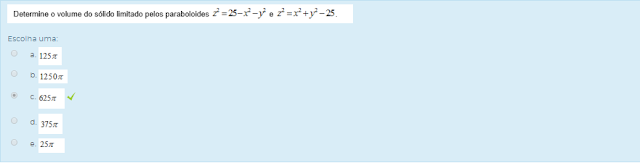
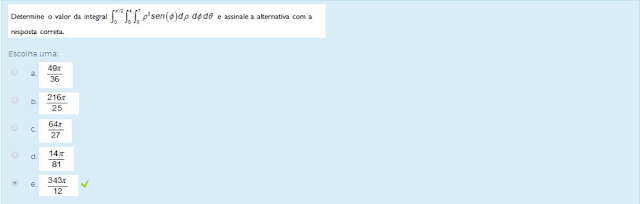
1) Assinale a alternativa que apresenta o valor da integral: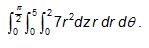

Escolha uma:

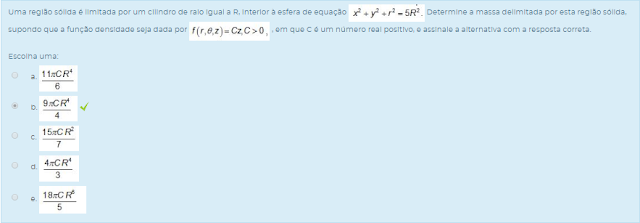
2) Uma região sólida é limitada por um cilindro de raio igual a R, interior à esfera de equação x²+y²+r²=5R² Determine a massa delimitada por esta região sólida, supondo que a função densidade seja dada por f(R,0,Z)=Cz,C>0 , em que C é um número real positivo, e assinale a alternativa com a resposta correta.

Escolha uma:

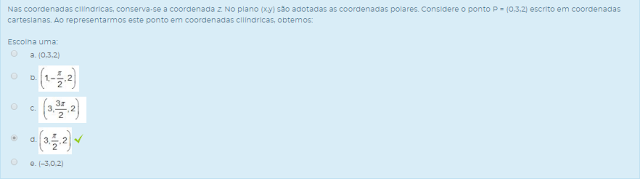
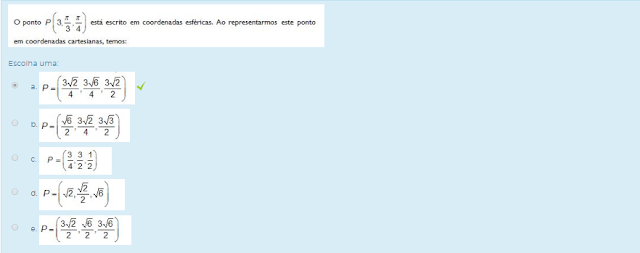
3) Nas coordenadas cilíndricas, conserva-se a coordenada z. No plano (x,y) são adotadas as coordenadas polares. Considere o ponto P = (0,3,2) escrito em coordenadas cartesianas. Ao representarmos este ponto em coordenadas cilíndricas, obtemos:

Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U2 - SEÇÃO 2 U2 S2 - ATIVIDADE DE APRENDIZAGEM
1) 

Escolha uma:

2) 

Escolha uma:

3) 
Escolha uma:

 CÁLCULO DIFERENCIAL E INTEGRAL III U2 - SEÇÃO 3 U2 S3 - ATIVIDADE DIAGNÓSTICA

1) 

Escolha uma:

2) 
Escolha uma:

3) 
Escolha uma:

 CÁLCULO DIFERENCIAL E INTEGRAL III U2 - SEÇÃO 3 U2 S3 - ATIVIDADE DE APRENDIZAGEM

 

1)

Escolha uma:


2) A equação do cilindro x²+y²=16 em coordenadas esféricas é:


Escolha uma: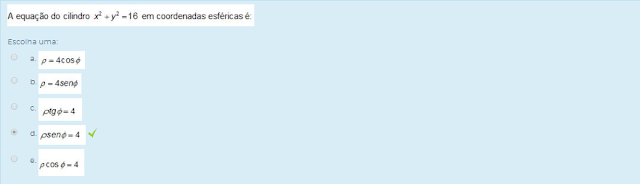



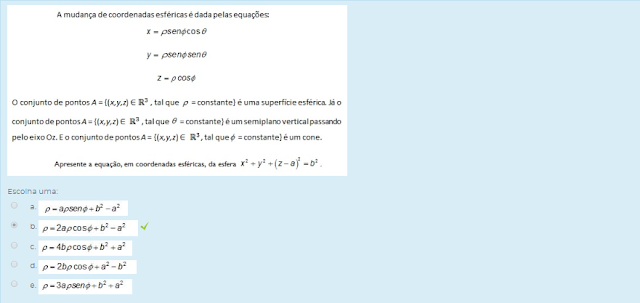
3) Apresenta a equação, em coordenadas esféricas, da esfera x²+y²+(z-1)²=1.


Escolha uma: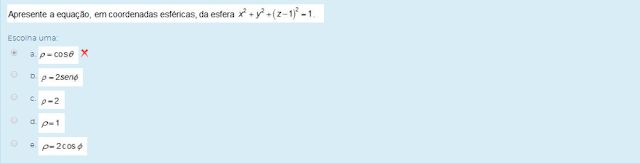




Tipo 2




1) Apresente a expressão, em coordenadas esféricas, para a integral de f (p,teta,0) sobre a região limitada pelo cone Z^2 = 3(x^2+y^2) e pelos pianos z = a e z = b. Suponha 0 < a < b.

Escolha uma: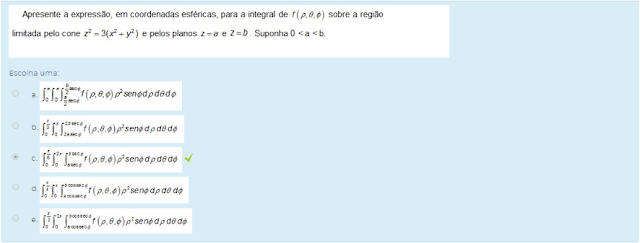



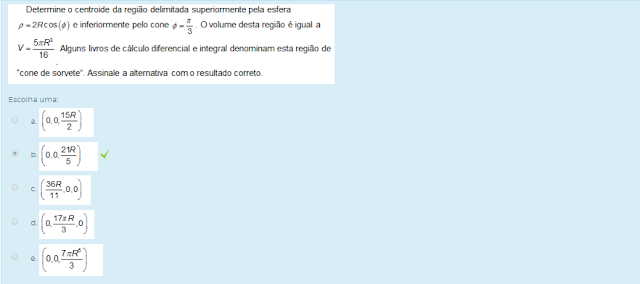
2)
Escolha uma:


3)
Escolha uma:

 CÁLCULO DIFERENCIAL E INTEGRAL III U2 - SEÇÃO 4 U2 S4 - ATIVIDADE DIAGNÓSTICA

 1)


Escolha uma:

2) 


Escolha uma:

3) Determine a massa da esfera de raio a. Suponha que a função densidade seja constante e igual a K. Assinale a alternativa com a resposta correta.
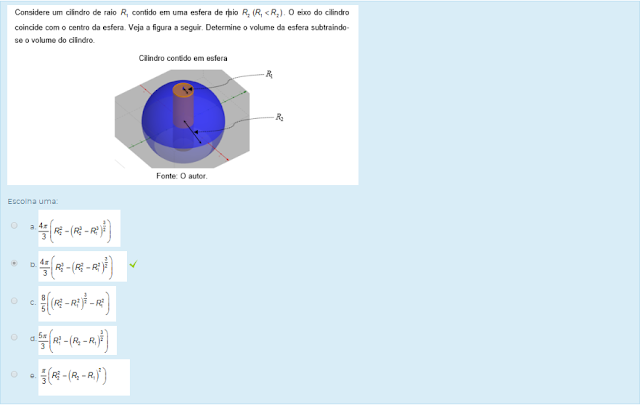
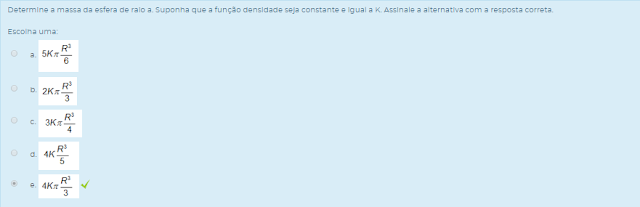
Escolha uma:

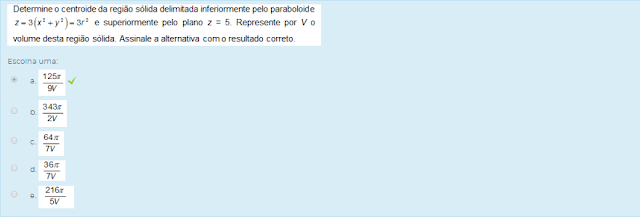
 CÁLCULO DIFERENCIAL E INTEGRAL III U2 - SEÇÃO 4 U2 S4 - ATIVIDADE DE APRENDIZAGEM

 

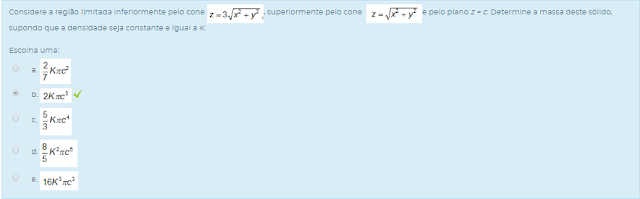
1) Considere a região limitada inferiormente pelo cone z=3raizx²+y², superiormente pelo cone z=raiz x²+y²e pelo plano z = c. Determine a massa deste sólido, supondo que a densidade seja constante e igual a K.
Escolha uma:

2) Considere um cilindro de massa M, altura H e raio R. Se escrevermos o momento de inércia deste cilindro em termos da massa M e do raio R, teremos (considere densidade constante igual a 1):
Escolha uma:

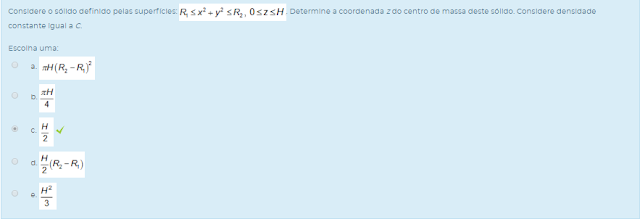
3) Considere o sólido definido pelas superfícies: . Determine a coordenada z do centro de massa deste sólido. Considere densidade constante igual a C. 
Escolha uma:

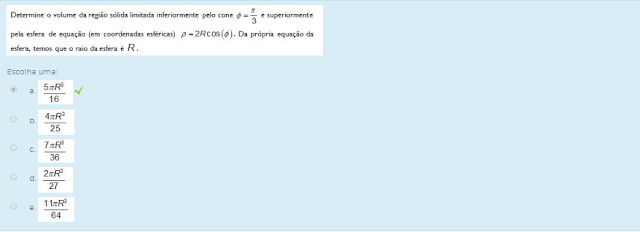
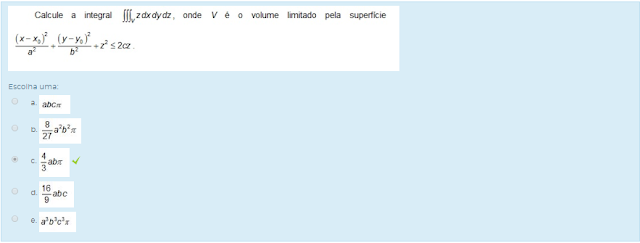
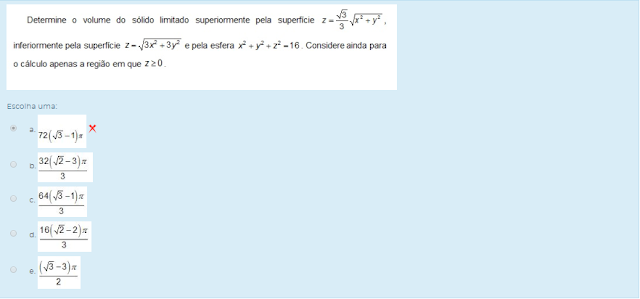
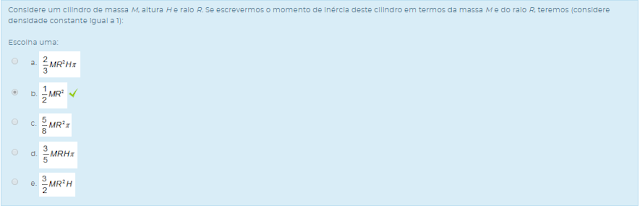
 CÁLCULO DIFERENCIAL E INTEGRAL III U2 - SEÇÃO 4 U2 - AVALIAÇÃO DA UNIDADE

 

1) 

Escolha uma:

2) 

Escolha uma :

3) O cálculo do momento de inércia é de extrema relevância em muitas subáreas da Engenharia. Seja em estruturas de engenharia civil ou em máquinas e equipamentos da engenharia mecânica, naval e aeronáutica, determinar a resistência a movimentos de rotação é muito importante para o correto projeto destes equipamentos e estruturas.



Escolha uma:

4) 


Escolha uma:

5) O momento de inércia possui grande importância em várias áreas da Engenharia. Ele mede a resistência a movimentos de rotação. Isso justifica o estudo de métodos para facilitar o cálculo de integrais múltiplas em problemas com simetrias específicas. Nessa situação entram em cena as mudanças de coordenadas retangulares para coordenadas cilíndricas e esféricas.


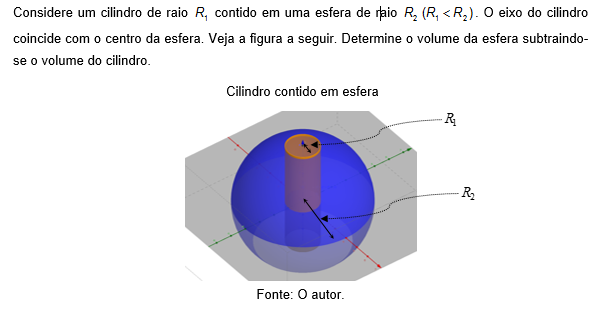
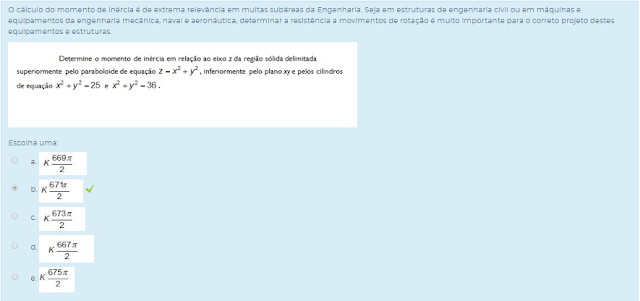
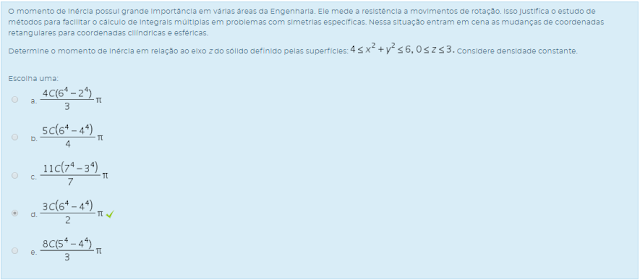
Determine o momento de inércia em relação ao eixo z do sólido definido pelas superfícies:  Considere densidade constante.
Escolha uma: