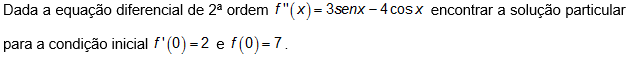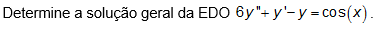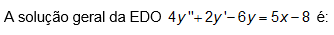CÁLCULO DIFERENCIAL E INTEGRAL III U3 - SEÇÃO 1 U3 S1 - ATIVIDADE DIAGNÓSTICA
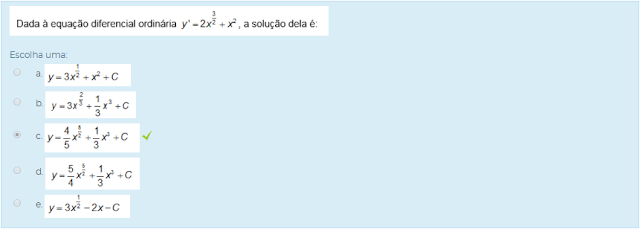
1) Dada à equação ordinária y=2x^³/² + x², a solução dela é:
Escolha uma:
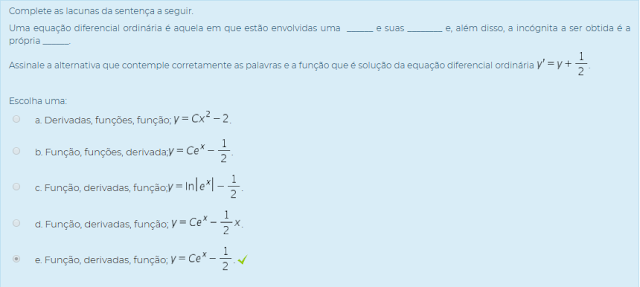
Uma equação diferencial ordinária é aquela em que estão envolvidas uma ______ e suas ________ e, além disso, a incógnita a ser obtida é a própria ______.
Assinale a alternativa que contemple corretamente as palavras e a função que é solução da equação diferencial ordinária Y=Y+1/2.
Escolha uma:
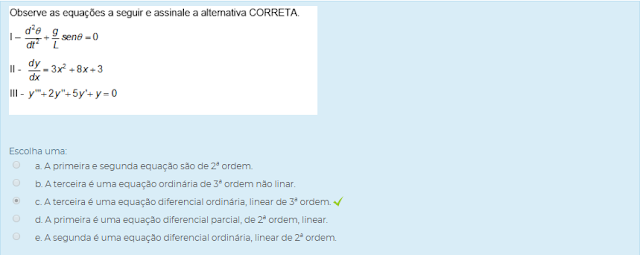
Escolha uma:
Escolha uma:
Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U3 - SEÇÃO 2 U3 S2 - ATIVIDADE DE APRENDIZAGEM
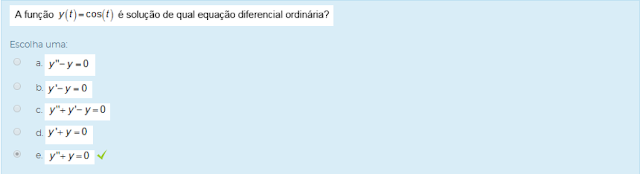
1) A função y(t)=cos(t) ´solução de qual equação diferencial ordinária?
Escolha uma:
2) A função y=x^4+2/3x³+x²/2+c, é solução geral de qual equação diferencial ordinária linear?
Escolha uma:

3) Assinale a alternativa CORRETA que contém a equação diferencial da velocidade, cuja função posição S(t)=3/2t²+4t+K é a sua solução.
Escolha uma:
CÁLCULO DIFERENCIAL E INTEGRAL III U3 - SEÇÃO 3 U3 S3 - ATIVIDADE DIAGNÓSTICA
1) Utilizando o método de equações diferenciais ordinárias homogêneas resolva a seguinte equação y'= x²+y²/xy.
Escolha uma:

2) Resolva a EDO yy'=x, determinando y (x) pelo método separação de variáveis.
Escolha uma: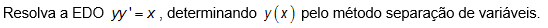

3) Determine a solução geral da equação diferencial ordinária linear de 1ª ordem y'-2y=e²x.
Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U3 - SEÇÃO 3 U3 S3 - ATIVIDADE DE APRENDIZAGEM
1) Verifique se as equações são homogêneas e assinale a alternativa CORRETA.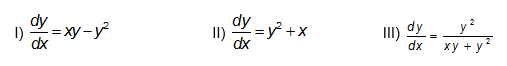
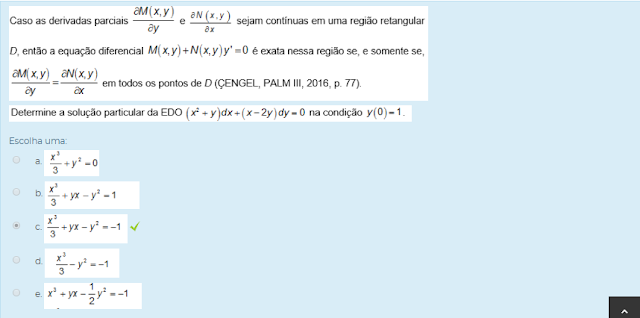
3) Na equação diferencial de 1ª ordem ( 2xy+1)+(x²+4y)y'=0, temos que M=2xy+1 e N=x²+4y. Sendo assim, é correto afirmar que:
CÁLCULO DIFERENCIAL E INTEGRAL III U3 - SEÇÃO 4 U3 S4 - ATIVIDADE DIAGNÓSTICA
1) Determine a solução geral homogênea da equação diferencial y"+2y'-8y=0.
Escolha uma:
2) Dada a equação diferencial de 2ª ordem f"(x)=3senx-4cosx encontrar a solução particular para a
condição inicial f'(0)=2 e f(0)=7.
Escolha uma:
3) Determine a solução geral da EDO 6y"+y'-y=cos(x).
Escolha uma:
CÁLCULO DIFERENCIAL E INTEGRAL III U3 - SEÇÃO 4 U3 S4 - ATIVIDADE DE APRENDIZAGEM
1) A solução geral da EDO 4y"+2y'-6y=5x-8 é:
Escolha uma:
2) Dada a solução geral y(x)=C1e-²x+c2e-³x, determine a solução particular com a condição inicial y(0)=2 e y'(0)=2.
Escolha uma:
3) Determine a solução geral homogênea da EDO 4y"-4y'+y=0.
Escolha uma:
CÁLCULO DIFERENCIAL E INTEGRAL III U3 - SEÇÃO 4 U3 - AVALIAÇÃO DA UNIDADE
1) Uma equação diferencial ordinária é aquela em que estão envolvidas a função e suas derivadas e, além disso, a incógnita a ser obtida é a própria função. São utilizadas em distintas áreas do conhecimento, onde através de modelos matemáticos, podemos lidar com diversas situações muito próximas das vivenciadas no cotidiano.
Qual será o saldo de uma conta poupança após um ano e meio, que começou com um depósito inicial de R$ 1.500,00 a uma taxa de 9% ao ano? Considere que nesse período não houve transações de saques ou depósitos.
Escolha uma:
Escolha uma: