CÁLCULO DIFERENCIAL E INTEGRAL III U1 - SEÇÃO 1 U1 S1 - ATIVIDADE DIAGNÓSTICA
1) Assinale a alternativa que contém o vetor normal à equação do plano 2x + 4y - z + d = 0.
Escolha uma:

2) Dada a superfície z = x2 + 3y2 + 4 = 0, assinale a alternativa que demonstra corretamente as derivadas parciais do vetor gradiente.
Escolha uma:

3) Para determinar a equação do plano e plano tangente, é preciso haver um vetor normal e um gradiente, respectivamente. Esses vetores formam um ângulo com os planos. Sendo assim, o ângulo referente a esses vetores é de:
Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U1 - SEÇÃO 1 U1 S1 - ATIVIDADE DE APRENDIZAGEM
1) Dada a equação do plano 3x + y - z - 3 = 0, e o ponto P(k,2,k-7), qual é o valor de k, para que este ponto pertença ao plano?
Escolha uma:

2) No produto escalar entre dois vetores, a.b=0 quando a ou b forem nulos, ou ainda:
Escolha uma:

3) Entre os vetores a seguir, qual possui as suas componentes definidas a partir de derivadas parciais?
Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U1 - SEÇÃO 2 U1 S2 - ATIVIDADE DIAGNÓSTICA
1) Sobre o teorema fundamental do cálculo, é correto afirmar que:
Escolha uma:

2) Dada a região R = {(x,y)|y = x2, y = x} representada pela figura,

As integrais sobre as regiões do tipo I e II correspondem, respectivamente, a:
Escolha uma:

3) O valor da Integral

é:
Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U1 - SEÇÃO 2 U1 S2 - ATIVIDADE DE APRENDIZAGEM
1) O teorema de Fubini é um recurso a fim de facilitar os cálculos das integrais. Tratando das integrais triplas, de quantas maneiras diferentes podemos fazer as integrações chegando sempre ao mesmo resultado?
Escolha uma:

2) Qual o valor da integral

onde

?
Escolha uma:

3) O processo de integral iterada é uma forma prática de resolver integrais. Desta forma, a integral

é igual a:
Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U1 - SEÇÃO 3 U1 S3 - ATIVIDADE DIAGNÓSTICA
1) Determine a massa de uma lâmina, dada pela integral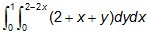 , onde (2 + x + y) representa a variação da densidade.
, onde (2 + x + y) representa a variação da densidade.

2) Nas integrais triplas, quando a densidade é constante, chamamos o centro de massa do sólido de centroide, onde os seus momentos de inércia estão relacionados aos eixos coordenados no plano tridimensional. Desta forma, podemos afirmar que o ly pode ser expresso por:
Escolha uma:

3) Assinale a alternativa CORRETA que contém a localização do centro de massa em uma determinada região.
Dados:

Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U1 - SEÇÃO 3 U1 S3 - ATIVIDADE DE APRENDIZAGEM
1) Suponha um sólido representado pela integral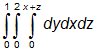 cuja função densidade é p(x,y,z) = 3xz. Assinale a alternativa correta correspondente ao momento no plano xy.
cuja função densidade é p(x,y,z) = 3xz. Assinale a alternativa correta correspondente ao momento no plano xy.
Escolha uma:

2) Qual a massa do sólido representado pela integral

cuja função densidade é p(x,y,z) = 3xz?
Escolha uma:

3) Nos estudos sobre integrais triplas, aprendemos o caso especial f(x,y,z). Desta forma, assinale a alternativa correta que representa o volume da região em formato de paralelepípedo com dimensões [2,5]x[1,2]x[1,3].
Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U1 - SEÇÃO 4 U1 S4 - ATIVIDADE DIAGNÓSTICA
1) Derivando a função z(x,y) = x2y - y3 + 5x2y2 em relação a x e y, respectivamente, temos:
Escolha uma:

2) Dada a superfície z + 4x - 5y = 1, a sua representação paramétrica é:
Escolha uma:

3) Sendo

e

, o produto vetorial entre eles e seu respectivo módulo é:
Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U1 - SEÇÃO 4 U1 S4 - ATIVIDADE DE APRENDIZAGEM
1) O módulo do produto vetorial entre dois vetores é igual à área do seguinte polígono:
Escolha uma:

2) Considere uma superfície derivável S e os vetores tangentes à superfície

e

. Um elemento infinitesimal de área é dado por

. Desta forma, ao calcularmos a área total de uma superfície, estamos somando as áreas:
Escolha uma:

3) Quando uma função f estiver expressa por z= f(x,y), para calcularmos a área da superfície de seu gráfico por meio da expressão:
Escolha uma:

CÁLCULO DIFERENCIAL E INTEGRAL III U1 - SEÇÃO 4 U1 - AVALIAÇÃO DA UNIDADE
1) A derivada parcial de uma função z = f(x,y) em relação a x considera apenas x como variável, mantendo y constante. Analogamente temos que a derivada parcial em relação a y considera apenas y como variável, mantendo x constante. Dessa forma, podemos entender que ela é obtida considerando-se apenas uma variável de cada vez, podendo ser escrita por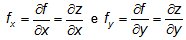 Sendo assim, ao derivarmos a função z(x,y) = 4x2y3 + x2y para determinar fx = (1,1) e fy = (-2,2), obteremos, respectivamente:
Sendo assim, ao derivarmos a função z(x,y) = 4x2y3 + x2y para determinar fx = (1,1) e fy = (-2,2), obteremos, respectivamente:
Escolha uma:

2) O produto escalar entre dois vetores pode ser representado por U.V (lemos U escalar V, e o seu resultado será sempre um valor numérico. Vale lembrar que, de acordo com o ângulo formado entre eles, esse valor poderá ser positivo (se o ângulo formado entre eles for agudo, ou seja, α < 90º), negativo (se o ângulo formado entre eles for obtuso, ou seja, α > 90º) ou nulo (se o ângulo formado entre eles for reto, ou seja, α = 90º).
Para que o produto escalar entre dois vetores seja nulo, os dois precisam ser ortogonais, diferentes de zero ou:
Escolha uma:

3) A integral definida representa a área de uma curva, a dupla representa o volume sob uma superfície e a tripla representa um hipervolume (quatro dimensões), que caracteriza um objeto de difícil visualização. Entre algumas aplicações direcionadas à integral tripla, podemos citar a densidade de uma região E(p(x,y,z)), que é dada em unidades de massa por unidade de volume em qualquer ponto (x,y,z). Para calcularmos a sua massa, devemos utilizar a lei matemática

Quando a densidade é constante, determinamos o momento de inércia de um sólido em relação aos eixos coordenados e chamamos o centro de massa desse sólido de:
Escolha uma:

4) O produto escalar entre dois vetores pode ser representado por U.V (lemos U escalar V, e o seu resultado será sempre um valor numérico. Vale lembrar que, de acordo com o ângulo formado entre eles, esse valor poderá ser positivo (se o ângulo formado entre eles for agudo, ou seja, α < 90º), negativo (se o ângulo formado entre eles for obtuso, ou seja, α > 90º) ou nulo (se o ângulo formado entre eles for reto, ou seja, α = 90º).
Para que o produto escalar entre dois vetores seja nulo, os dois precisam ser ortogonais, diferentes de zero ou:
Escolha uma:

5) Matematicamente, temos que o produto vetorial entre dois vetores a e b resulta em um terceiro vetor c. Ou seja, (a.b=c, que é perpendicular ao plano formado pelos vetores a e b. O sentido desse novo vetor gerado é dado por um recurso utilizado quando precisamos diferenciar ou estabelecer um padrão entre duas orientações espaciais possíveis. Este recurso foi originalmente estabelecido pelo físico John Ambrose Fleming, que o nomeou com o seu sobrenome, chamando-o assim de regra de Fleming.
Esta regra é popularmente conhecida como:
Escolha uma:


 é igual a:
é igual a:
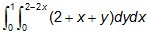 , onde (2 + x + y) representa a variação da densidade.
, onde (2 + x + y) representa a variação da densidade.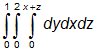 cuja função densidade é p(x,y,z) = 3xz. Assinale a alternativa correta correspondente ao momento no plano xy.
cuja função densidade é p(x,y,z) = 3xz. Assinale a alternativa correta correspondente ao momento no plano xy. cuja função densidade é p(x,y,z) = 3xz?
cuja função densidade é p(x,y,z) = 3xz? e
e . Um elemento infinitesimal de área é dado por
. Um elemento infinitesimal de área é dado por . Desta forma, ao calcularmos a área total de uma superfície, estamos somando as áreas:
. Desta forma, ao calcularmos a área total de uma superfície, estamos somando as áreas: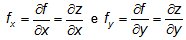 Sendo assim, ao derivarmos a função z(x,y) = 4x2y3 + x2y para determinar fx = (1,1) e fy = (-2,2), obteremos, respectivamente:
Sendo assim, ao derivarmos a função z(x,y) = 4x2y3 + x2y para determinar fx = (1,1) e fy = (-2,2), obteremos, respectivamente: Quando a densidade é constante, determinamos o momento de inércia de um sólido em relação aos eixos coordenados e chamamos o centro de massa desse sólido de:
Quando a densidade é constante, determinamos o momento de inércia de um sólido em relação aos eixos coordenados e chamamos o centro de massa desse sólido de:









































